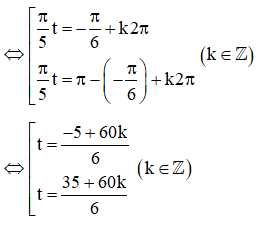Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán

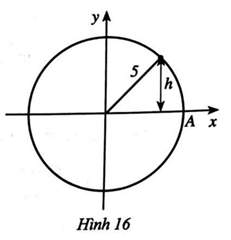
Bài 74 trang 33 SBT Toán 11 Tập 1: Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm. Khoảng cách h (cm) từ chất điểm đến trục hoành được tính theo công thức h = |y|, trong đó $y=a\sin \left(\frac{\pi }{5}t\right)$  với t là thời gian chuyển động của chất điểm tính bằng giây (t ≥ 0) và chất điểm bắt đầu chuyển động từ vị trí A (Hình 16).

a) Chất điểm chuyển động một vòng hết bao nhiêu giây?

b) Tìm giá trị của a.

c) Tìm thời điểm sao cho chất điểm ở vị trí có h = 2,5 cm và nằm phía dưới trục hoành trong một vòng quay đầu tiên.

Trả lời

a) Xét h = 0 hay |y| = 0, suy ra y = 0, tức là $a\sin \left(\frac{\pi }{5}t\right)=0$ $\iff \sin \left(\frac{\pi }{5}t\right)=0$

$\iff \frac{\pi }{5}t=k\pi \left(k\in \mathbb{Z}\right)$ $\iff t=5k\left(k\in \mathbb{Z},k\ge 0\right)$ (do t ≥ 0).

Ta nhận thấy, từ thời điểm ban đầu, cứ sau 5 giây, khoảng cách từ chất điểm đến trục hoành lại bằng 0. Suy ra sau mỗi 5 giây, chất điểm chuyển động được nửa vòng. Vậy chất điểm chuyển động một vòng hết 10 giây.

b) Do chất điểm chuyển động một vòng hết 10 giây nên khi t = 2,5 giây thì chất điểm chuyển động được một phần tư vòng theo chiều dương, suy ra tại t = 2,5 ta có y = |y| = h = 5 (do bằng bán kính). Khi đó, $a\sin \left(\frac{\pi }{5}\mathrm{.2,5}\right)=5$ $\iff a=5$.

Vậy a = 5.

c) Từ kết quả câu b, ta có: $y=5\sin \left(\frac{\pi }{5}t\right)$.

Do h = 2,5 cm và chất điểm nằm ở dưới trục hoành nên y = – 2,5.

Với y = – 2,5, ta có: $5\sin \left(\frac{\pi }{5}t\right)=-\mathrm{2,5}$

$\iff \sin \left(\frac{\pi }{5}t\right)=-\frac{1}{2}$

$\iff \sin \left(\frac{\pi }{5}t\right)=\sin \left(-\frac{\pi }{6}\right)$

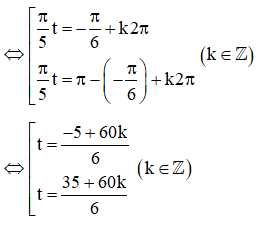
Với vòng quay đầu tiên thì 0 ≤ t ≤ 10, do đó $t=\frac{35}{6},t=\frac{55}{6}$ .

Vậy tại thời điểm $t=\frac{35}{6}$  giây, $t=\frac{55}{6}$  giây thì chất điểm ở vị trí có h = 2,5 cm và nằm ở dưới trục hoành trong một vòng quay đầu tiên.

Xem thêm lời giải bài tập SBT Toán 11 Cánh diều hay, chi tiết khác:

Bài 3: Hàm số lượng giác và đồ thị

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân