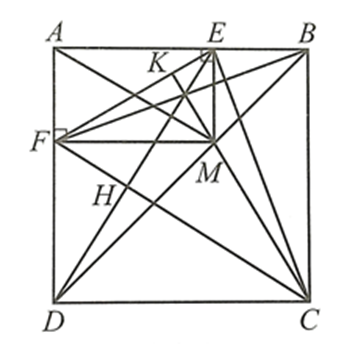
Xác định vị trí của điểm M trên đường chéo BD để diện tích của tứ giác AEMF lớn nhất.
Cho hình vuông ABCD. Lấy điểm M thuộc đường chéo BD. Kẻ ME vuông góc với AB tại E, MF vuông góc với AD tại F.
Xác định vị trí của điểm M trên đường chéo BD để diện tích của tứ giác AEMF lớn nhất.