Đường thẳng qua D và song song với AE cắt AH tại F. Tứ giác ADFE là hình gì Vì sao
36
18/08/2024
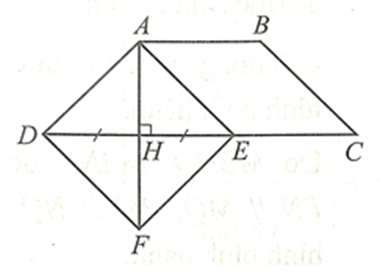
Cho hình thang cân ABCD có AB // CD, ˆD=45∘. Kẻ AH vuông góc với CD tại H. Lấy điểm E thuộc cạnh CD sao cho HE = DH.
Đường thẳng qua D và song song với AE cắt AH tại F. Tứ giác ADFE là hình gì? Vì sao?
Trả lời
Do DF // AE nên ^FDH=^AEH (hai góc so le trong).
Xét ∆FDH và ∆AEH có:
^DHF=^AHE=90∘, ^FDH=^AEH, DH = HE
Do đó ∆FDH = ∆AEH (cạnh huyền – góc nhọn)
Suy ra AH = HF (hai cạnh tương ứng)
Hay H là trung điểm của AF
Tứ giác ADFE có hai đường chéo AF và DE vuông góc với nhau tại trung điểm H của mỗi đường nên ADFE là hình thoi.
Tam giác ADE có ^AED=^ADE=45∘ nên tam giác ADE vuông cân tại A, do đó ^DAE=90∘.
Hình thoi ADFE có ^DAE=90∘ nên là hình vuông.