Gọi P là giao điểm của AM và BN, Q là giao điểm của CN và DM. Chứng minh tứ giác
26
18/08/2024
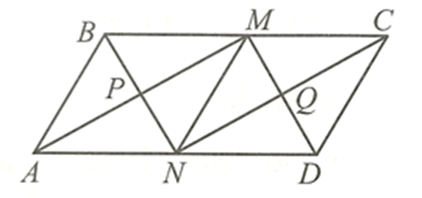
Cho hình bình hành ABCD có BC = 2AB. Gọi M, N lần lượt là trung điểm của BC, AD.
Gọi P là giao điểm của AM và BN, Q là giao điểm của CN và DM. Chứng minh tứ giác PMQN là hình chữ nhật.
Trả lời
Tương tự câu a, ta chứng minh được MANC là hình bình hành.
Do MBND, MANC đều là hình bình hành nên PN // MQ, PM // NQ (do P là giao điểm của AM và BN, Q là giao điểm của CN và DM).
Suy ra tứ giác PMQN là hình bình hành.
Xét ∆ABN và ∆MNB có:
AN = BM, ^ANB=^MBN(hai góc so le trong do BM // AN), cạnh BN chung
Do đó ∆ABN = ∆MNB (c.g.c). Suy ra AB = MN (hai cạnh tương ứng0
Tứ giác ABMN có AB = BM = MN = AN nên ABMN là hình thoi.
Suy ra AM ⊥ BN, do đó ^MPN=90∘.
Hình bình hành PMQN có ^MPN=90∘ nên PMQN là hình chữ nhật.