Chứng minh ba đường thẳng DE, BF, CM cùng đi qua một điểm
Cho hình vuông ABCD. Lấy điểm M thuộc đường chéo BD. Kẻ ME vuông góc với AB tại E, MF vuông góc với AD tại F.
Chứng minh ba đường thẳng DE, BF, CM cùng đi qua một điểm.
Cho hình vuông ABCD. Lấy điểm M thuộc đường chéo BD. Kẻ ME vuông góc với AB tại E, MF vuông góc với AD tại F.
Chứng minh ba đường thẳng DE, BF, CM cùng đi qua một điểm.
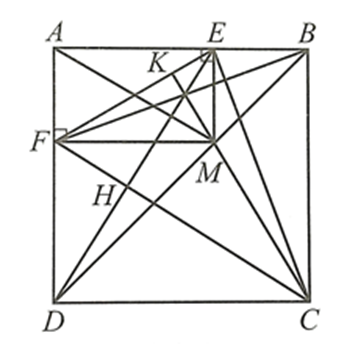
Gọi H là giao điểm của DE và CF, K là giao điểm của CM và EF.
Do ABCD là hình vuông nên ta có: ^DAB=90∘,CD=DA,^ADB=^ABD=^DBC=45∘
Tương tự câu a, ta chứng minh được BF ⊥ CE.
Xét ∆ABM và ∆CBM có:
AB = BC, ^ABM=^CBM(=45∘), cạnh BM chung
Do đó ∆ABM = ∆CBM (c.g.c)
Suy ra AM = CM (hai cạnh tương ứng)
Mà EF = AM (vì AEMF là hình chữ nhật), suy ra EF = CM.
Xét ∆DEF và ∆FCM có:
DE = FC, EF = CM, DF = FM
Do đó ∆DEF = ∆FCM (c.c.c)
Suy ra ^DEF=^FCM (hai góc tương ứng)
Hay ^FEH=^FCK.
Trong tam giác HEF vuông tại H, ta có ^FEH+^EFH=90∘.
Suy ra ^FCK+^EFH=90∘ hay ^FCK+^KFC=90∘.
Do đó ^CKF=90∘. Do đó CK ⊥ EF.
Trong tam giác CEF, ta có: EH ⊥ CF, FB ⊥ CE, CM ⊥ EF nên ba đường thẳng EH, FB, CM là các đường cao của tam giác CEF.
Hay ba đường thẳng DE, BF, CM là các đường cao của tam giác CEF.
Vậy ba đường thẳng DE, BF, CM cùng đi qua một điểm.