Cho hình thang cân ABCD có AB // CD Chứng minh tứ giác ABCE là hình bình hành
Cho hình thang cân ABCD có AB // CD, ˆD=45∘. Kẻ AH vuông góc với CD tại H. Lấy điểm E thuộc cạnh CD sao cho HE = DH.
Chứng minh tứ giác ABCE là hình bình hành.
Cho hình thang cân ABCD có AB // CD, ˆD=45∘. Kẻ AH vuông góc với CD tại H. Lấy điểm E thuộc cạnh CD sao cho HE = DH.
Chứng minh tứ giác ABCE là hình bình hành.
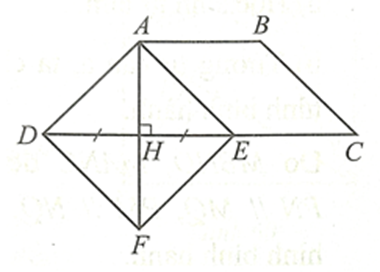
Do ABCD là hình thang cân nên AB // CD và ˆC=^ADC=45∘
Xét ∆ADH vuông tại H và ∆AEH vuông tại H có:
DH = EH, cạnh AH chung
Do đó ∆ADH = ∆AEH (hai cạnh góc vuông)
Suy ra ^ADH=^AEH (hai góc tương ứng)
Hay ^ADC=^AED.
Mà ˆC=^ADC nên ˆC=^AED.
Lại có ˆC,^AED nằm ở vị trí đồng vị, suy ra AE // BC.
Tứ giác ABCE có AB // CE, AE // BC nên ABCE là hình bình hành.