Cho hình vuông ABCD. Lấy điểm M Chứng minh: DE = CF; DE vuông góc CF
Cho hình vuông ABCD. Lấy điểm M thuộc đường chéo BD. Kẻ ME vuông góc với AB tại E, MF vuông góc với AD tại F.
Chứng minh: DE = CF; DE ⊥ CF.
Cho hình vuông ABCD. Lấy điểm M thuộc đường chéo BD. Kẻ ME vuông góc với AB tại E, MF vuông góc với AD tại F.
Chứng minh: DE = CF; DE ⊥ CF.
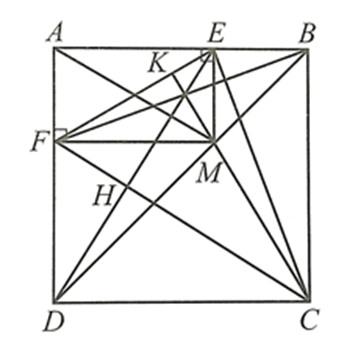
Gọi H là giao điểm của DE và CF, K là giao điểm của CM và EF.
Do ABCD là hình vuông nên ta có: ^DAB=90∘,CD=DA,^ADB=^ABD=^DBC=45∘
Do MF ⊥ AD nên tam giác FDM vuông tại F.
Do FM ⊥ AD, DC ⊥ AD nên FM // CD, suy ra ^FMD=^MDC (hai góc so le trong)
Mà ^FDM=^MDC (do ABCD là hình vuông nên DM là phân giác góc ADC)
Suy ra ^FDM=^FMD, nên ∆FDM cân tại F
Do đó FM = FD.
Do ME ⊥ AB nên ^MEA=90∘
Tứ giác AEMF có ^MFA=^FAE=^AEM=90∘ nên AEMF là hình chữ nhật.
Suy ra AE = FM.
Do đó AE = FD (vì cùng bằng FM).
Xét ∆ADE vuông tại A và ∆DCF vuông tại D có:
AE = DF, AD = DC (chứng minh trên)
Do đó ∆ADE = ∆DCF (hai cạnh góc vuông)
Suy ra DE = CF (hai cạnh tương ứng) và ^AED=^DFC (hai góc tương ứng)
Xét tam giác ADE vuông tại A, ta có: ^AED+^ADE=90∘.
Suy ra ^DFC+^ADE=90∘ hay ^DFH+^FDH=90∘.
Xét ∆DHF có ^DFH+^FDH+^DHF=180∘
Suy ra ^DHF=180∘−(^DFH+^FDH)=180∘−90∘=90∘.
Vậy DE ⊥ CF.