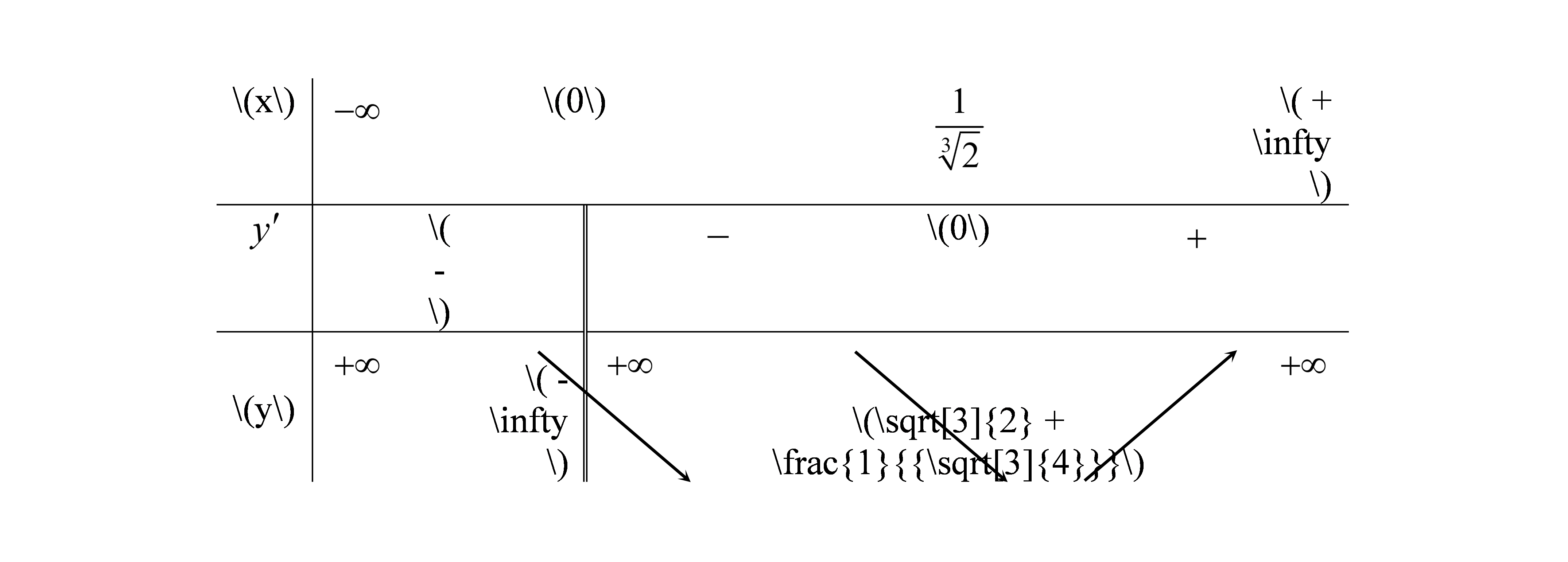Với giá trị nào của x thì hàm số y = x^2 + 1/x đạt giá trị nhỏ nhất trên khoảng ( 0; + vô cùng)?      A. 3/ căn bậc hai của 34    B. 1/ căn bậc hai của 2      C. 1    D. 1 /căn bậc hai của 3

Trả lời

Chọn D

TXD: $D = \mathbb{R}\backslash \left\{ 0 \right\}$.

$y' = 2x - \frac{1}{{{x^2}}}$, $y' = 0 \Leftrightarrow x = \frac{1}{{\sqrt[3]{2}}}.$

Dựa vào BBT thì $x = \frac{1}{{\sqrt[3]{2}}}$ hàm số đạt giá trị nhỏ nhất trên $\left( {0; + \infty } \right)$.