Vẽ AE vuông góc với BD tại E. Chứng minh rằng $\widehat {BEH} = \widehat {BAH}$.

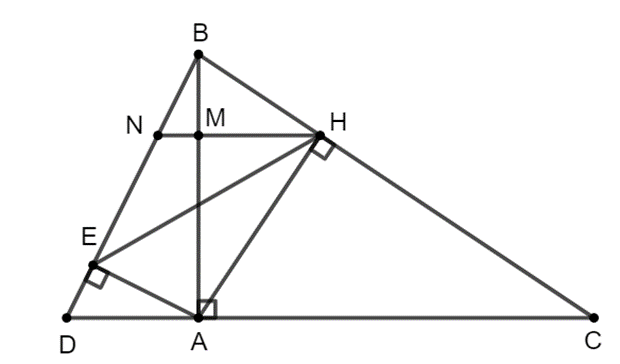
Xét ∆ABD vuông tại A và ∆EBA vuông tại E có $\widehat {ABD}$ chung.

Do đó ∆ABD ᔕ ∆EBA (g.g).

Suy ra $\frac{{AB}}{{BE}} = \frac{{BD}}{{AB}}$. Do đó AB² = BD . BE.

Mà AB² = BC . BH nên BC . BH = BD . BE.

Do đó $\frac{{BH}}{{BD}} = \frac{{BE}}{{BC}}$.

Xét ∆BEH và ∆BCD có

$\frac{{BH}}{{BD}} = \frac{{BE}}{{BC}}$ và $\widehat {DBC}$ chung.

Do đó ∆BEH ᔕ ∆BCD (c.g.c).

Suy ra $\widehat {BEH} = \widehat {BCD}$ (hai góc tương ứng).

Mà $\widehat {BAH} = \widehat {BCD}$ (cùng phụ với $\widehat {HAC}$).

Do đó $\widehat {BEH} = \widehat {BAH}$ (đpcm).