Cho tam giác ABC vuông tại A Trên tia đối của tia AC lấy điểm D (AD < AC
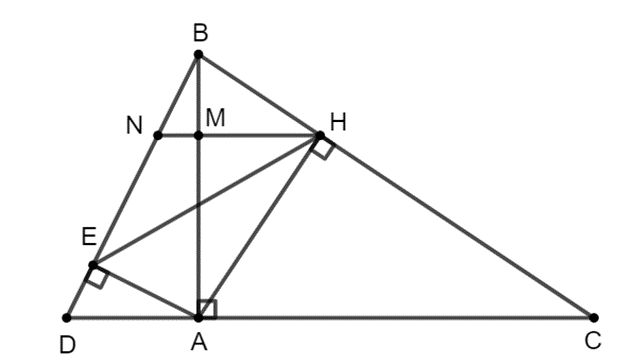
Cho tam giác ABC vuông tại A và đường cao AH.
Trên tia đối của tia AC lấy điểm D (AD < AC). Đường thẳng qua H và song song với AC cắt AB, BD lần lượt tại M, N. Chứng minh rằng \[\frac{{MN}}{{MH}} = \frac{{AD}}{{AC}}\].