Trên đoạn HB lầy điểm I sao cho góc AIC = 90 độ. Chứng minh rằng AI^2
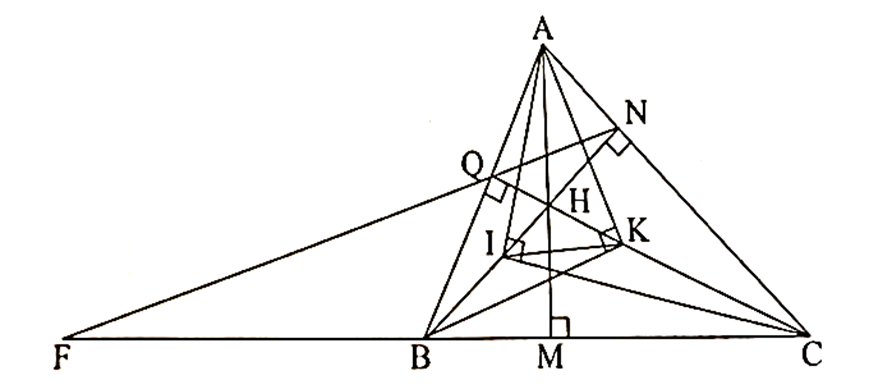
Cho tam giác nhọn ABC có ba đường cao AM, BN, CQ cắt nhau tại H.
Trên đoạn HB lầy điểm I sao cho \[\widehat {AIC} = 90^\circ \]. Chứng minh rằng AI2 = AN . AC.
Xét ∆ANI vuông tại N và ∆AIC vuông tại I có \[\widehat {IAC}\]chung.
Do đó ∆ANI ᔕ ∆AIC (g.g).
Suy ra \[\frac{{AN}}{{AI}} = \frac{{AI}}{{AC}}\]. Do đó AI2 = AN . AC (1)