Đường thẳng QN cắt đường thẳng BC tại F. Chứng minh rằng FB . FC = FQ . FN
Cho tam giác nhọn ABC có ba đường cao AM, BN, CQ cắt nhau tại H.
Đường thẳng QN cắt đường thẳng BC tại F. Chứng minh rằng FB . FC = FQ . FN.
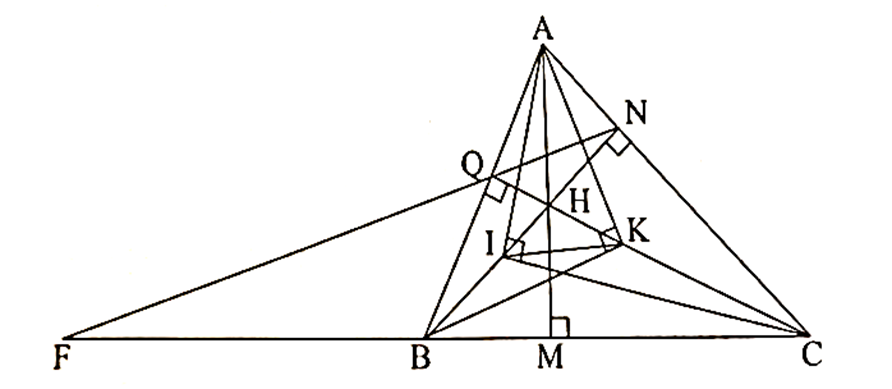
Xét ∆FQB và ∆FCN có
\[\widehat {CFN}\] chung; \[\widehat {FQB} = \widehat {FCN}\] \[\left( { = \widehat {AQN}} \right)\].
Do đó ∆FQB ᔕ ∆FCN (g.g).
Suy ra \[\frac{{FQ}}{{FC}} = \frac{{FB}}{{FN}}\]. Do đó FB . FC = FQ . FN (g.g).