Cho tam giác nhọn ABC Chứng mình rằng: AD . BH = AC . BD
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H. Chứng mình rằng:
AD . BH = AC . BD.
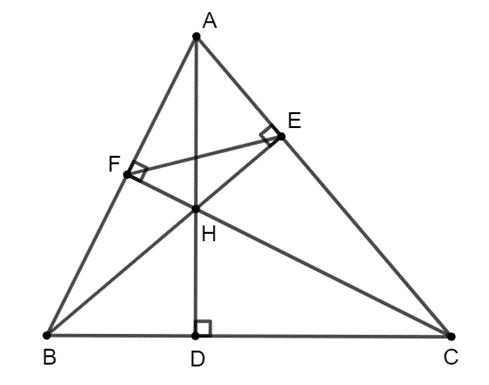
Ta có \[\widehat {AHE} = \widehat {ACD}\] ( cùng phụ với \[\widehat {CAD}\]).
Mà \[\widehat {AHE} = \widehat {BHD}\] (đối đỉnh) nên \[\widehat {ACD} = \widehat {BHD}\].
Xét ∆ADC vuông tại D và ∆BDH vuông tại D có \[\widehat {ACD} = \widehat {BHD}\].
Do đó ∆ADC ᔕ ∆BDH (g.g).
Suy ra \[\frac{{AD}}{{BD}} = \frac{{AC}}{{BH}}\]. Do đó AD . BH = AC . BD (đpcm).