Cho tam giác nhọn ABC Chứng minh rằng tam giác ANQ đồng dạng tam giác ABC
Cho tam giác nhọn ABC có ba đường cao AM, BN, CQ cắt nhau tại H.
Chứng minh rằng ∆ANQ ᔕ ∆ABC.
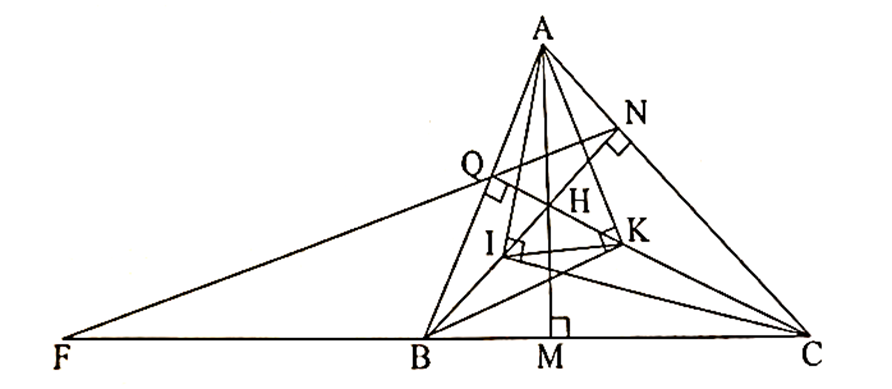
Xét ∆ANB vuông tại N và ∆AQC vuông tại Q có \[\widehat {BAC}\] chung.
Do đó ∆ANB ᔕ ∆AQC (g.g).
Suy ra \[\frac{{AN}}{{AQ}} = \frac{{AB}}{{AC}}\] hay \[\frac{{AN}}{{AB}} = \frac{{AQ}}{{AC}}\].
Xét ∆ANQ và ∆ABC có
\[\frac{{AN}}{{AB}} = \frac{{AQ}}{{AC}}\]; \[\widehat {BAC}\] chung.
Do đó ∆ANQ ᔕ ∆ABC (c.g.c)