BC² = BE . BH + CF . CH.

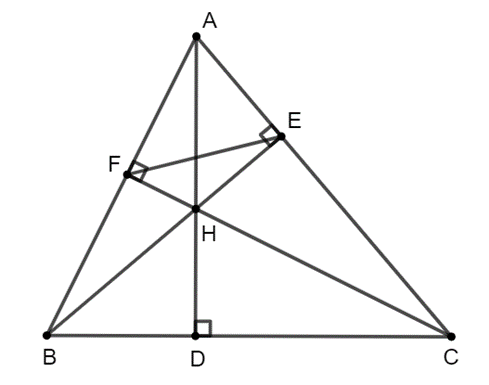
Xét ∆BEC vuông tại E và ∆BHD vuông tại D có \[\widehat {EBC}\] chung.

Do đó ∆BEC ᔕ ∆BHD (g.g).

Suy ra \[\frac{{BC}}{{BH}} = \frac{{BE}}{{BD}}\]. Do đó BC . BD = BE . BH     (3)

Xét ∆BCF vuông tại F và ∆HCD vuông tại D có \[\widehat {FCB}\] chung.

Do đó ∆BCF ᔕ ∆HCD (g.g)

Suy ra \[\frac{{BC}}{{HC}} = \frac{{CF}}{{DC}}\]. Do đó BC . DC = CF . HC. (4)

Từ (3) và (4), suy ra BC . DB + BC . DC = BE . BH + CF . HC.

Do đó BC² = BE . BH + CF . CH (đpcm).