Trên đoạn HC lấy điểm K sao cho góc AKB = 90 độ. Chứng minh rằng tam giác AIK
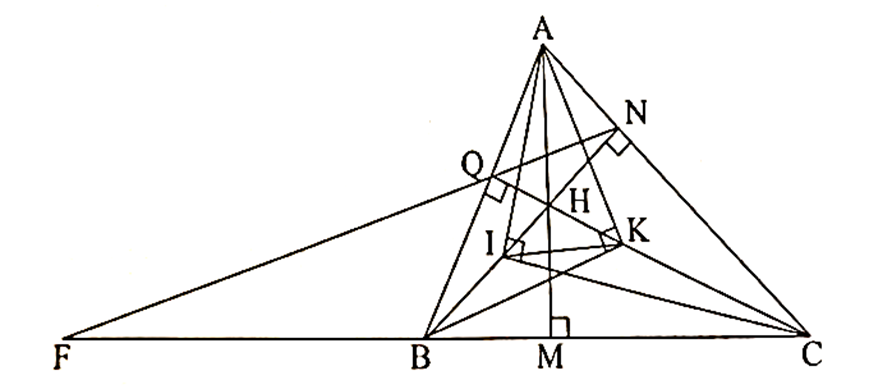
Cho tam giác nhọn ABC có ba đường cao AM, BN, CQ cắt nhau tại H.
Trên đoạn HC lấy điểm K sao cho \[\widehat {AKB} = 90^\circ \]. Chứng mình rằng ∆AIK cân.
Xét ∆AQK vuông tại Q và ∆AKB vuông tại K có \[\widehat {BAK}\] chung.
Do đó ∆AQK ᔕ ∆AKB (g.g).
Suy ra \[\frac{{AQ}}{{AK}} = \frac{{AK}}{{AB}}\]. Do đó AK2 = AQ . AB (2)
Mà \[\frac{{AN}}{{AB}} = \frac{{AQ}}{{AC}}\] nên suy ra AN . AC = AQ . AB (3)
Từ (1), (2) và (3) suy ra AI = AK.
Vậy nên ∆AIK cân tại A.