Từ một tấm tôn hình chữ nhất có chiều dài và rộng là 60cm, 40cm. Người ta cắt đi 6 hình
27
30/04/2024
Từ một tấm tôn hình chữ nhất có chiều dài và rộng là 60cm, 40cm. Người ta cắt đi 6 hình vuông cạnh \(x\left( {cm} \right)\) rồi gấp tấm tôn còn lại để được một cái hộp có nắp như hình vẽ dưới đây. Tìm x để hộp nhận được có thể tích lớn nhất.
A. \(\frac{{20}}{3}\left( {cm} \right)\)
B. \(\frac{{10}}{3}\left( {cm} \right)\)
C. \(4\left( {cm} \right)\)
D. \(5\left( {cm} \right)\)
Trả lời
Đáp án A
Phương pháp:
Lập hàm số tính thể tích khối hộp theo biến x, khảo sát tìm x để hộp nhận được có thể tích lớn nhất.
Cách giải:
Sau khi cắt, độ dài 2 chiều của đáy là: \(40 - 2x,\,\,\,\frac{{60 - 3x}}{2}\left( {cm} \right),\,\,x \in \left( {0;20} \right)\)
Thể tích khối hộp: \(V = x\left( {40 - 2x} \right).\frac{{60 - 3x}}{2} = 3x{\left( {20 - x} \right)^2} = f\left( x \right)\)
\(f'\left( x \right) = 3{\left( {20 - x} \right)^2} - 3x.2\left( {20 - x} \right) = 3 = 3.\left( {20 - x} \right)\left( {20 - 3x} \right)\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 20\left( L \right)\\x = \frac{{20}}{3}\end{array} \right.\)
Bảng biến thiên:
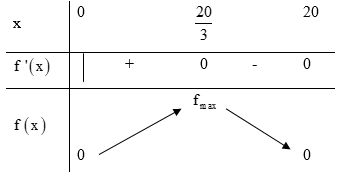
Vậy \(x = \frac{{20}}{3}\) thì hộp nhận được có thể tích lớn nhất.
