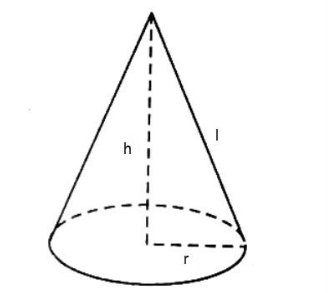
Hình nón có chiều cao bằng đường kính đáy. Tỉ số thể tích giữa diện tích xung quanh
Hình nón có chiều cao bằng đường kính đáy. Tỉ số thể tích giữa diện tích xung quanh và diện tích toàn phần của hình nón là:
A. \(\frac{1}{2}\)
B. \(\frac{{1 + \sqrt 5 }}{4}\)
C. \(\frac{1}{4}\)
D. \(\frac{{5 - \sqrt 5 }}{4}\)