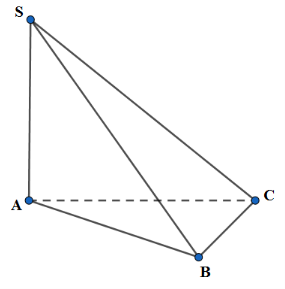
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA = a và vuông góc với đáy
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, \(SA = a\) và vuông góc với đáy. Thể tích V của khối chóp S.ABC theo a là:
A. \({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{{12}}\)
B. \({V_{S.ABC}} = \frac{{{a^3}\sqrt 2 }}{{12}}\)
C. \({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{3}\)
D. \({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{4}\)