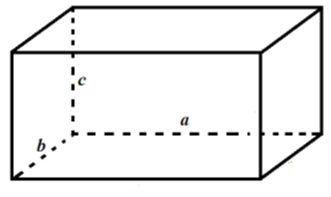
Diện tích toàn phần của một hình hộp chữ nhật là Stp = 8a^2. Đáy của hình hộp là hình vuông cạnh
Diện tích toàn phần của một hình hộp chữ nhật là \({S_{tp}} = 8{a^2}\). Đáy của hình hộp là hình vuông cạnh a. Tính thể tích V của khối hộp theo a.
D. \(V = \frac{7}{4}{a^3}\)