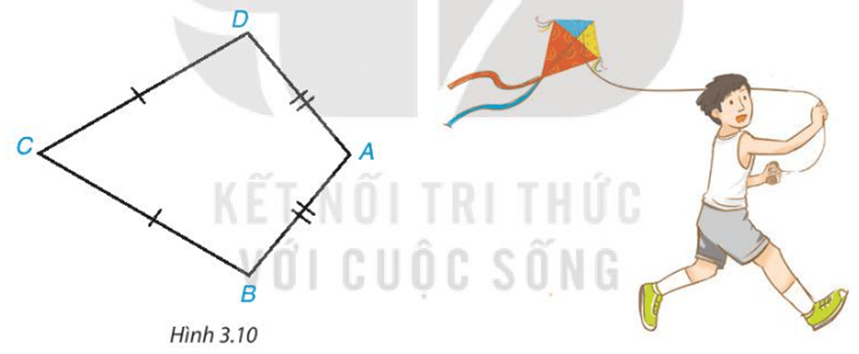
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”

Bài 3.3 trang 51 Toán 8 Tập 1: Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.

b) Tính các góc B, D biết rằng $\hat{A}=100°,\hat{C}=60°$ .

Trả lời

a) Nối AC, BD (như hình vẽ).

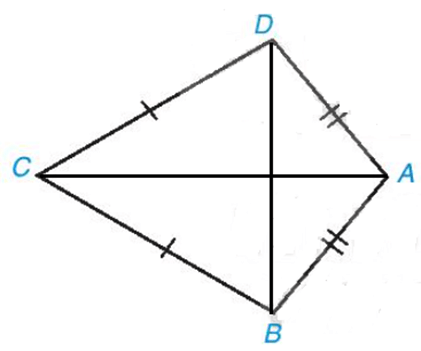
Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;

CB = CD hay hai điểm C cách đều hai đầu mút B và D;

Do đó, hai điểm A và C cách đều hai đầu mút B và D.

Vậy AC là đường trung trực của đoạn thẳng BD.

b) Gọi I là giao điểm của AC và BD.

Vì AC là đường trung trực của đoạn thẳng BD nên AC ⊥ BD.

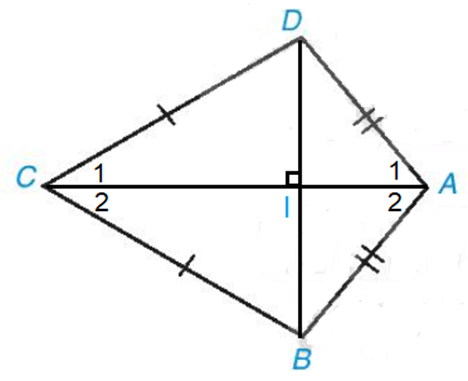
• Xét tam giác ABD cân tại A (vì AB = AD) có AI là đường cao (vì AI ⊥ BD)

Nên AI cũng là tia phân giác của $\widehat{BAD}$ hay ${\hat{A}}_1={\hat{A}}_2$ .

Suy ra ${\hat{A}}_1={\hat{A}}_2=\frac{\widehat{BAD}}{2}=\frac{100°}{2}=50°$ .

• Xét tam giác BCD cân tại C (vì BC = CD) có CI là đường cao (vì AC ⊥ BD)

Nên CI cũng là tia phân giác của $\widehat{BCD}$ hay ${\hat{C}}_1={\hat{C}}_2$ .

Suy ra null .

• Xét tam giác ACD có: ${\hat{A}}_1+{\hat{C}}_1+\widehat{ADC}=180°$ (định lí tổng ba góc trong một tam giác).

Hay $50°+30°+\widehat{ADC}=180°$ .

Suy ra $\widehat{ADC}=180°-50°-30°=100°$ .

Xét tứ giác ABCD có: $\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360°$ (định lí tổng ba góc trong một tam giác).

Hay $100°+\widehat{ABC}+60°+100°=360°$ .

Suy ra $\widehat{ABC}+260°=360°$ .

Do đó $\widehat{ABC}=360°-260°=100°$ .

Vậy $\widehat{ABC}=100°$ ; $\widehat{ADC}=100°$ .

Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung trang 45

Bài tập cuối chương 2