Giải SGK Toán 8 (Kết nối tri thức) Luyện tập chung trang 56 Tập 1

Giải SGK Toán 8 Luyện tập chung trang 56 Tập 1

Bài tập

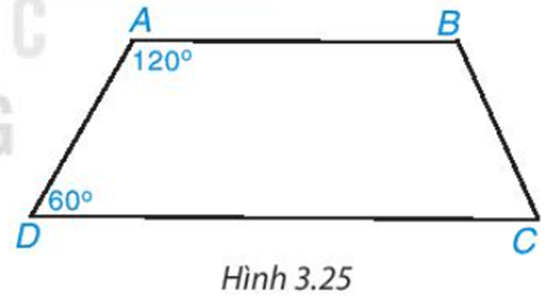
Bài 3.9 trang 56 Toán 8 Tập 1: Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?

Lời giải:

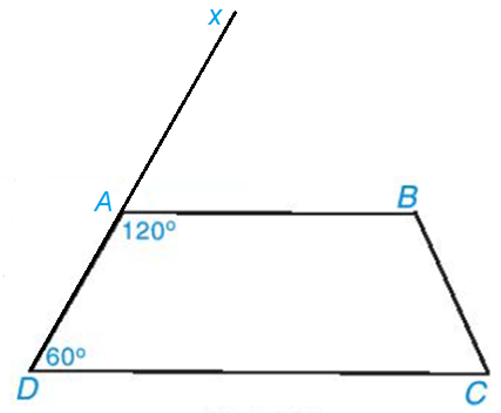
Vẽ tia Dx đi qua điểm A.

Vì $\widehat{DAB}$ và $\widehat{BAx}$ là hai góc kề bù nên $\widehat{DAB}+\widehat{BAx}=180°$ .

Suy ra $\widehat{BAx}=180°-\widehat{DAB}=180°-120°=60°$ .

Ta có $\widehat{ADC}=\widehat{BAx}=60°$ mà hai góc này ở vị trí đồng vị nên AB // CD.

Vậy tứ giác ABCD là hình thang.

Bài 3.10 trang 56 Toán 8 Tập 1: Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết $\widehat{ABD}=30°$ , tính số đo các góc của hình thang đó.

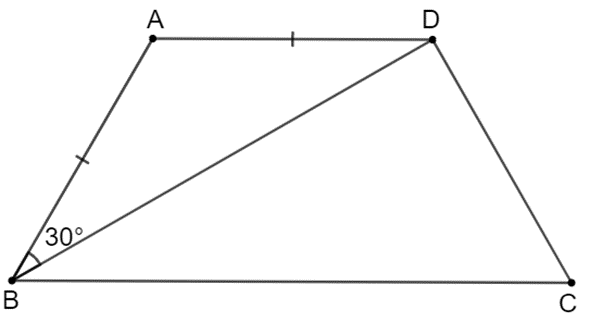
Lời giải:

Xét tam giác ABD cân tại A (vì AB = AD), ta có:

• $\widehat{ADB}=\widehat{ABD}=30°$ ;

• $\hat{A}+\widehat{ABD}+\widehat{ADB}=180°$ hay $\hat{A}+30°+30°=180°$

Suy ra $\hat{A}=180°-30°-30°=120°$ .

Vì AB // CD nên null (hai góc so le trong).

Do đó $\widehat{ABC}=\widehat{ABD}+\widehat{CBD}=30°+30°=60°$ .

Vì tứ giác ABCD là hình thang cân nên $\hat{C}=\widehat{ABC}=60°$ ; $\widehat{ADC}=\hat{A}=120°$ .

Vậy số đo các góc của hình thang cân ABCD là $\hat{A}=120°$ ; $\widehat{ABC}=60°$ ; $\hat{C}=60°$ ; $\widehat{ADC}=120°.$

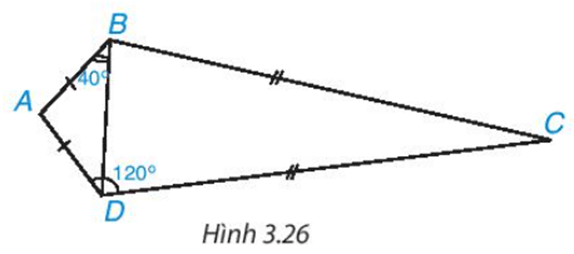
Bài 3.11 trang 56 Toán 8 Tập 1: Tính số đo các góc của tứ giác ABCD trong Hình 3.26.

Lời giải:

* Xét tam giác ABD cân tại A (vì AB = AD) ta có:

• $\widehat{ADB}=\widehat{ABD}=40°$ .

• $\hat{A}+\widehat{ABD}+\widehat{ADB}=180°$ .

Suy ra $\hat{A}=180°-\widehat{ABD}-\widehat{ADB}=180°-40°-40°=100°$ .

Ta có $\widehat{ADB}+\widehat{BDC}=120°$ suy ra $\widehat{BDC}=120°-\widehat{ADB}=120°-40°=80°$ .

* Xét tam giác BCD cân tại C (vì BC = CD) ta có:

• $\widehat{CBD}=\widehat{CDB}=80°$ .

• $\hat{C}+\widehat{CBD}+\widehat{CDB}=180°$

Suy ra $\hat{C}=180°-\widehat{CBD}-\widehat{CDB}=180°-80°-80°=20°$ .

Ta có: $\widehat{ABC}=\widehat{ABD}+\widehat{CBD}=40°+80°=120°$ .

Vậy số đo các góc của tứ giác ABCD là $\hat{A}=100°$ ; $\widehat{ABC}=120°$ ; $\hat{C}=20°$ .

Bài 3.12 trang 56 Toán 8 Tập 1: Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.

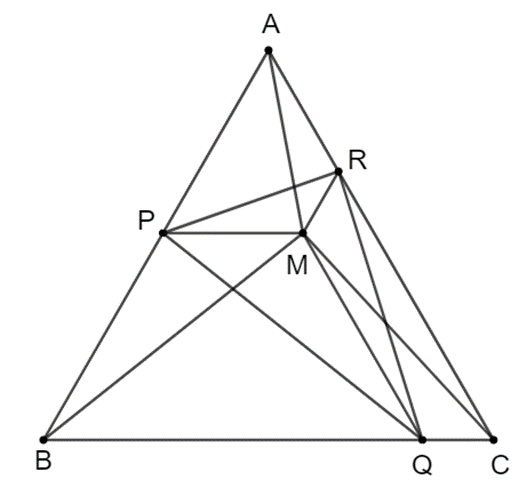
a) Chứng minh tứ giác APMR là hình thang cân.

b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.

c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?

Lời giải:

a) Vì tam giác ABC đều nên $\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60°$ .

Vì PM // BC nên $\widehat{APM}=\widehat{ABC}=60°$ (đồng vị).

Suy ra $\widehat{APM}=\widehat{PAR}$ (cùng bằng 60°).

Tứ giác APMR là hình thang (vì MR // AP) có $\widehat{APM}=\widehat{PAR}$.

Do đó tứ giác APMR là hình thang cân.

b) Vì tứ giác APMR là hình thang cân nên AM = PR (1)

Chứng minh tương tự câu a, ta cũng có các tứ giác BPMQ và MQCR là hình thang cân.

Suy ra BM = PQ và MC = QR (2)

Từ (1)và (2) suy ra PR + PQ + QR = MA + MB + MC.

Mà PR + PQ + QR chính là chu vi của tam giác PQR.

Do đó chu vi tam giác PQR bằng tổng độ dài MA + MB + MC (đpcm).

c) Để tam giác PQR là tam giác đều thìPR = PQ = QRsuy ra MA = MB = MC

Khi đó điểm M cách đều ba đỉnh A, B, C của tam giác ABC.

Do đó M là giao điểm của ba đường trung trực (đồng thời M cũng là giao điểm của ba đường trung tuyến, ba đường cao, đường phân giác).

Vậy khi M là giao điểm của ba đường trung trực thì tam giác PQR là tam giác đều.