Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2). a) Chứng minh ABCD là một hình vuông
349
13/06/2023
Bài 1 trang 73 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2).
a) Chứng minh ABCD là một hình vuông.
b) Tìm tọa độ tâm I của hình vuông ABCD.
Trả lời
Ta có: →AB = (-1; 3) ⇒ AB = √(−1)2+32=√10
→DC = (-1; 3) ⇒ DC = √(−1)2+32=√10
⇒ →AB=→DC ⇒ AB // CD và AB = DC
⇒ ABCD là hình bình hành (1)
Ta lại có: →AD = (3; 1)
⇒ →AB.→AD = (-1).3 + 3.1 = 0
⇒ →AB⊥→AD
⇒ ^BAD=90° (2)
Từ (1) và (2) suy ra ABCD là hình vuông.
b) Vì I là tâm của hình vuông ABCD nên I là giao điểm của hai đường cheoc AC và BD hay I là trung điểm của AC. Khi đó tọa độ điểm I là:
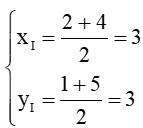 ⇒ I(3; 3).
⇒ I(3; 3).
Vậy tọa độ tâm I của hình vuông ABCD là I(3; 3).
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài tập cuối chương 9
Bài 1: Không gian mẫu và biến cố
Bài 2: Xác suất của biến cố
Bài tập cuối chương 10

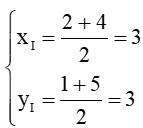 ⇒ I(3; 3).
⇒ I(3; 3).