Cổng trào của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (Hình 3). Từ một điểm M trên thân cổng
576
13/06/2023
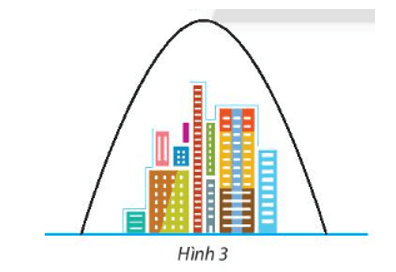
Bài 17 trang 75 Toán lớp 10 Tập 2: Cổng trào của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (Hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2m và khoảng cách từ chân đường vuông góc vẽ từ M xuống mặt đất đến cổng gần nhất là 0,5 m. Tính chiều cao của cổng.
Trả lời
Ta có hệ trục tọa độ như hình vẽ:
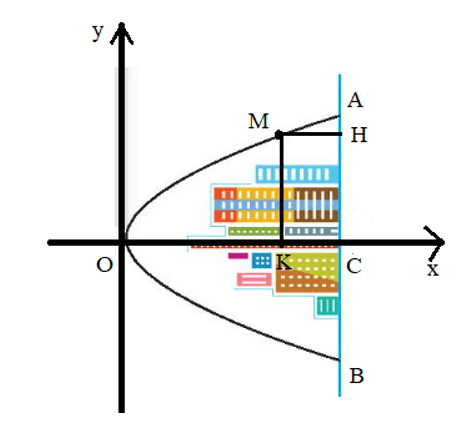
Phương trình parabol (P) có dạng y2 = 2px.
Gọi chiều cao của cổng là h (m) ⇒ OC = h
Ta có khoảng cách đến mặt đất là 2m nên MH = 2 ⇒ OK = h – 2 và khoảng cách từ chân đường vuông góc vẽ từ M xuống mặt đất đến cổng gần nhất là 0,5 m nên AH = 0,5.
Ta lại có khoảng cách giữa hai chân cổng là 192 m nên AC = 192:2 = 96.
Khi đó tọa độ điểm A là A(h; 96)
Mà AH + CH = AC
⇒ CH = AC – AH = 96 – 0,5 = 95,5
⇒ M(h – 2; 95,5).
Vì các điểm M và A thuộc parabol nên tọa độ của M và A đều thỏa mãn phương trình y2 = 2px, ta có:
962 = 2ph (1) và 95,52 = 2p(h – 2) (2)
Chia vế với vế của (1) cho (2) ta được:
96295,52=hh−2
⇔ 9 216(h – 2) = 9 120,25h
⇔ 9 216h – 18 432 = 9 120,25h
⇔ 95,75h = 18 432
⇔ h ≈ 192,5 (m)
Vậy chiều cao của cổng khoảng 192,5m.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài tập cuối chương 9
Bài 1: Không gian mẫu và biến cố
Bài 2: Xác suất của biến cố
Bài tập cuối chương 10


