Viết phương trình chính tắc của parabol thỏa mãn từng điều kiện sau: a) Tiêu điểm (4; 0)

Bài 14 trang 74 Toán lớp 10 Tập 2: Viết phương trình chính tắc của parabol thỏa mãn từng điều kiện sau:

a) Tiêu điểm (4; 0);

b) Đường chuẩn có phương trình x = $-\frac{1}{6}$;

c) Đi qua điểm (1; 4);

d) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 8.

Trả lời

a) Tiêu điểm F(4; 0)

⇒ $\frac{p}{2}=4$ ⇔ p = 8

Suy ra phương trình chính tắc của parabol là: y² = 2px = 2.8.x = 16x.

Vậy phương trình chính tắc của parabol cần tìm là y² = 16x.

b) Đường chuẩn có phương trình x = $-\frac{1}{6}$ ⇔ x + $\frac{1}{6}$ = 0

⇒ $\frac{p}{2}=\frac{1}{6}$ ⇔ p = $\frac{1}{3}$

Suy ra phương trình chính tắc của parabol là: y² = 2px = 2.$\frac{1}{3}$.x = $\frac{2}{3}$x.

Vậy phương trình chính tắc của parabol cần tìm là y² = $\frac{2}{3}$x.

c) Phương trình chính tắc của parabol cần tìm là: y² = 2px

Vì parabol đi qua điểm (1; 4) nên tọa độ điểm này thỏa mãn phương trình trên, ta có:

4² = 2.p.1

⇔ 16 = 2p

⇔ p = 8

Suy ra phương trình chính tắc của parabol cần tìm là: y² = 2.8.x = 16x.

Vậy phương trình chính tắc của parabol cần tìm là: y² = 16x.

d) Gọi tiêu điểm F$\left(\frac{p}{2};0\right)$ và đường chuẩn của parabol cần tìm là ∆: x + $\frac{p}{2}$ = 0.

Áp dụng công thức tính khoảng cách từ điểm đến đường thẳng, ta có:

d(F; ∆) =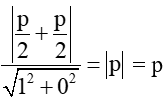 

Mà khoảng cách từ tiêu điểm đến đường chuẩn bằng 8 nên p = 8

Suy ra phương trình chính tắc của parabol cần tìm là: y² = 2.8.x = 16x.

Vậy phương trình chính tắc của parabol cần tìm là: y² = 16x.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Đường tròn trong mặt phẳng toạ độ

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố

Bài tập cuối chương 10