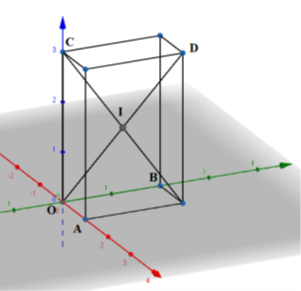
Trong không gian Oxyz, cho bốn điểm \(A\left( {1;0;0} \right),\,\,B\left( {0;2;0} \right),\,\,C\left( {0;0;3} \right),\,\,D\left( {1;2;3} \right)\). Phương trình mặt cầu đi qua bốn điểm A, B, C, D là:

B. \({x^2} + {y^2} + {z^2} - x - 2y - 3z - 14 = 0\)

D. \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z = 0\)

Đáp án A

Phương pháp:

Bốn điểm đã cho là 4 đỉnh của một hình hộp chữ nhật, nên tâm mặt cầu đi qua 4 điểm đó chính là tâm của hình hộp chữ nhật.

Cách giải:

Bốn điểm \[{\rm{A}}\left( {1;0;0} \right),\,\,B\left( {0;2;0} \right),\,\,C\left( {0;0;3} \right),\,\,D\left( {1;2;3} \right)\] là 4 đỉnh của một hình hộp chữ nhật, nên tâm mặt cầu đi qua 4 điểm đó chính là tâm của hình hộp chữ nhật và là trung điểm của OD.

\( \Rightarrow \) Tâm của hình hộp chữ nhật đó là: \(I\left( {\frac{1}{2};1;\frac{3}{2}} \right)\)

\(OD = \sqrt {{1^2} + {2^2} + {3^2}} = \sqrt {14} \Rightarrow \) Bán kính mặt cầu là \(R = \frac{{OD}}{2} = \frac{{\sqrt {14} }}{2}\)

Phương trình mặt cầu: \({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {x - \frac{3}{2}} \right)^2} = {\left( {\frac{{\sqrt {14} }}{2}} \right)^2} \Leftrightarrow {x^2} + {y^2} + {z^2} - x - 2y - 3z = 0\)