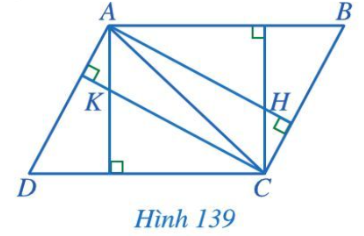
Trong Hình 139, cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm các tam giác ABC và ACD. Chứng minh AK // CH và AH // CK

Bài 5 trang 118 Toán 7 Tập 2: Trong Hình 139, cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm các tam giác ABC và ACD. Chứng minh AK // CH và AH // CK.

Trả lời

Chứng minh (Hình 139):

+) Vì K là trực tâm của tam giác ACD (giả thiết) nên AK $\perp$ CD.

Mà AB // CD (giả thiết) nên AK $\perp$ AB.

Vì H là trực tâm của tam giác ABC (giả thiết) nên CH $\perp$ AB.

Do đó AK // CH.

+) Vì K là trực tâm của tam giác ACD (giả thiết) nên CK $\perp$ AD.

Mà AD // BC (giả thiết) nên CK $\perp$ BC.

Vì H là trực tâm của tam giác ABC (giả thiết) nên AH $\perp$ BC.

Do đó AH // CK.