Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực

Bài 6 trang 118 Toán 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:

a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;

b) Nếu tam giác ABC có hai điểm H, I trùng nhau thì tam giác ABC là tam giác đều.

Trả lời

a)

Chứng minh (Hình vẽ dưới đây):

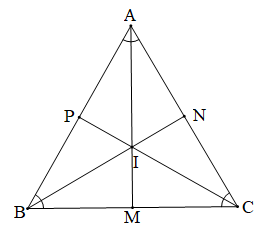
Kéo dài AI cắt BC tại M, kéo dài BI cắt AC tại N, kéo dài CP cắt AB tại P.

Khi đó AM là đường phân giác của $\widehat{BAC}$ nên $\widehat{BAM}=\widehat{CAM};$

Do tam giác ABC đều nên AB = BC = CA.

Xét $∆$ABM và $∆$ACM có:

AB = AC (chứng minh trên),

$\widehat{BAM}=\widehat{CAM}$ (chứng minh trên),

AM là cạnh chung

Do đó $∆$ABM = $∆$ACM  (c.g.c).

Suy ra:

• $\widehat{AMB}=\widehat{AMC}$ (hai góc tương ứng);

• BM = CM (hai cạnh tương ứng).

Vì BM = CM nên M là trung điểm của BC.

Ta có $\widehat{AMB}=\widehat{AMC}$, mà $\widehat{AMB}+\widehat{AMC}=180°$ nên $\widehat{AMB}=\widehat{AMC}=\frac{180°}{2}=90°$.

Khi đó AM $\perp$ BC tại trung điểm M của BC nên AM là đường trung trực của đoạn thẳng BC cũng đồng thời là đường cao và đường trung tuyến kẻ từ A của $∆$ABC.

Chứng minh tương tự ta cũng có:

+) BN là đường trung trực của đoạn thẳng AC, đồng thời là đường cao và đường trung tuyến kẻ từ B của $∆$ABC.

+) CP là đường trung trực của đoạn thẳng AB, đồng thời là đường cao và đường trung tuyến kẻ từ C của $∆$ABC.

Mà AM, BN, CP cắt nhau tại I nên G, H, I, O trùng nhau.

b)

Chứng minh (Hình vẽ dưới đây):

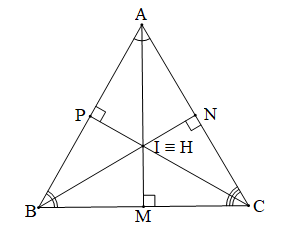
Vì I là giao điểm ba đường phân giác, H là trực tâm của tam giác ABC (giả thiết) nên:

+ AI là đường phân giác và AH là đường cao kẻ từ A của $∆$ABC.

Mà I ≡ H (giả thiết) nên đường phân giác AI trùng với đường cao AH.

+ Tương tự đường phân giác BI trùng đường cao BH;

+ Đường phân giác CI trùng đường cao CH.

Gọi M, N, P lần lượt là chân đường cao (hay cũng chính là đường phân giác) kẻ từ A, B, C đến BC, CA, AB.

Xét $∆$ABM (vuông tại M) và $∆$ACM (vuông tại M) có:

$\widehat{BAM}=\widehat{CAM}$ (do AM là tia phân giác của $\widehat{BAC}$),

AM là cạnh chung

Do đó $∆$ABM = $∆$ACM (cạnh góc vuông – góc nhọn kề).

Suy ra AB = AC (hai cạnh tương ứng). (1)

Xét $∆$ABN (vuông tại N) và $∆$CBN (vuông tại N) có:

BN là cạnh chung,

$\widehat{ABN}=\widehat{CBN}$ (do BN là tia phân giác của $\widehat{ABC}$),

Do đó $∆$ABN = $∆$CBN (cạnh góc vuông – góc nhọn kề).

Suy ra AB = BC (hai cạnh tương ứng). (2)

Từ (1) và (2) suy ra AB = BC = CA do đó tam giác ABC là tam giác đều.

Vậy tam giác ABC đều.