Tính thể tích V khối lập phương biết rằng khối cầu ngoại tiếp khối lập phương có thể tích là $\frac{{32}}{3}\pi$

D. $V = \frac{{8\sqrt 3 }}{3}$

Đáp án A

Phương pháp:

+) Thể tích khối cầu có bán kính R là: $V = \frac{4}{3}\pi {R^3}$

+) Thể tích khối lập phương có cạnh bằng a là: $V = {a^3}$

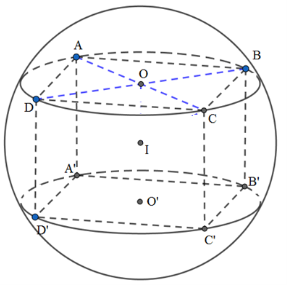
Giả sử khối lập phương ABCD.A’B’C’D’ có các cạnh đều bằng a.

Khi đó: $AC' = \sqrt {A{B^2} + A{D^2} + AA{'^2}} = \sqrt 3 a \Rightarrow R = \frac{{AC'}}{2} = \frac{{a\sqrt 3 }}{2}$

Thể tích khối cầu có bán kính R là: $V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^3} = \frac{{\sqrt 3 \pi {a^3}}}{2} = \frac{{32}}{3}\pi \Leftarrow a = \frac{4}{{\sqrt 3 }}$

Thể tích khối lập phương: $V = {a^3} = {\left( {\frac{4}{{\sqrt 3 }}} \right)^3} = \frac{{64}}{{3\sqrt 3 }} = \frac{\begin{array}{l}6\\64\sqrt 3 \end{array}}{9}$