Tính hiệu P(x) - Q(x) bằng hai cách, trong đó: P(x) = 6.x^3 + 8.x^2 + 5.x - 2

Luyện tập 4 trang 59 Toán 7 Tập 2: Tính hiệu P(x) - Q(x) bằng hai cách, trong đó:

P(x) = 6x³ + 8x² + 5x - 2;

Q(x) = -9x³ + 6x² + 3 + 2x.

Trả lời

Cách 1. Tính hiệu theo cột dọc:

Ta sắp xếp đa thức Q(x) theo số mũ giảm dần của biến x được:

Q(x) = -9x³ + 6x² + 3 + 2x

Q(x) = -9x³ + 6x² + 2x + 3.

Thực hiện tính hiệu P(x) – Q(x):

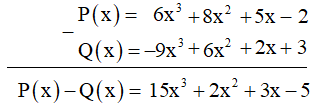
Vậy P(x) - Q(x) = 15x³ + 2x² + 3x - 5.

Cách 2. Tính hiệu theo hàng ngang:

P(x) - Q(x)

= 6x³ + 8x² + 5x - 2 - (-9x³ + 6x² + 3 + 2x)

= 6x³ + 8x² + 5x - 2 + 9x³ - 6x² - 3 - 2x

= (6x³ + 9x³) + (8x² - 6x²) + (5x - 2x) + (-2 - 3)

= 15x³ + 2x² + 3x - 5.

Vậy P(x) - Q(x) = 15x³ + 2x² + 3x - 5.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 1: Biểu thức số. Biểu thức đại số

Bài 2: Đa thức một biến. Nghiệm của đa thức một biến

Bài 3: Phép cộng, phép trừ đa thức một biến

Bài 4: Phép nhân đa thức một biến

Bài 5: Phép chia đa thức một biến

Bài tập cuối chương 6