D. \(R = \frac{a}{2}\)
Đáp án C
Phương pháp:
+) Xác định trục của mặt đáy (đường thẳng đi qua tâm đáy và vuông góc với đáy).
+) Xác định đường trung trực của một mặt bên.
+) Xác định giao điểm của hai đường thẳng trên.
Cách giải:
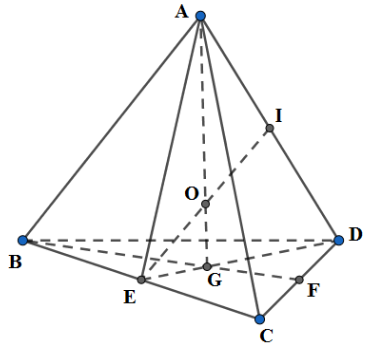
Gọi E, F, I lần lượt là trung điểm của BC, CD, AD; G là trọng tâm tam giác BCD; O là giao điểm của AG và EI.
* Ta chứng minh: O là tâm mặt cầu ngoại tiếp tứ diện ABCD:
Thật vậy:
Do tam giác BCD đều, G là trọng tâm \( \Rightarrow \) là tâm đường tròn ngoại tiếp G
Do tứ diện ABCD đều \( \Rightarrow AG \bot \left( {BCD} \right)\)
Điểm \(O \in AG \Rightarrow OB = OC = OD\,\,\left( 1 \right)\)
Do \(AE = DE \Rightarrow \Delta AED\) cân tại E \( \Rightarrow \) EI là trung trực của AD \( \Rightarrow OA = OD\,\,\left( 2 \right)\)
Từ (1), (2) \( \Rightarrow \) O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
* Tính bán kính đường tròn ngoại tiếp tứ diện ABCD:
\(\Delta BCD\) đều, cạnh bằng a \( \Rightarrow ED = \frac{{a\sqrt 3 }}{2} \Rightarrow EG = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6},\,\,\,GD = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
\(\Delta EID\) vuông tại I \( \Rightarrow EI = \sqrt {E{D^2} - I{D^2}} = \sqrt {\frac{3}{4}{a^2} - \frac{1}{4}{a^2}} = \frac{1}{{\sqrt 2 }}a\)
\(\Delta OEG\) đồng dạng \(\Delta DEI \Rightarrow \frac{{OG}}{{ID}} = \frac{{EG}}{{EI}} \Leftrightarrow \frac{{OG}}{{\frac{a}{2}}} = \frac{{\frac{{a\sqrt 3 }}{3}}}{{\frac{1}{{\sqrt 2 }}a}} = \frac{{\sqrt 6 }}{3} \Rightarrow OG = \frac{a}{{\sqrt 6 }}\)
\(\Delta OGD\) vuông tại G \( \Rightarrow OD = \sqrt {O{G^2} + G{D^2}} = \sqrt {\frac{1}{6}{a^2} + \frac{1}{3}{a^2}} = \frac{a}{{\sqrt 2 }} = \frac{{a\sqrt 2 }}{4}\)
Vậy, bán kính đường tròn ngoại tiếp tứ diện ABCD là \(R = \frac{{a\sqrt 2 }}{4}\)