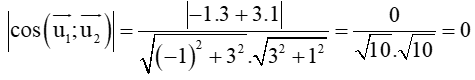Tìm tọa độ giao điểm và góc giữa hai đường thẳng d1 và d2 trong mỗi trường hợp sau: a) d1: x – y + 2 = 0 và d2: x + y + 4 = 0
944
13/06/2023
Bài 3 trang 73 Toán lớp 10 Tập 2: Tìm tọa độ giao điểm và góc giữa hai đường thẳng d1 và d2 trong mỗi trường hợp sau:
a) d1: x – y + 2 = 0 và d2: x + y + 4 = 0;
b) d1: 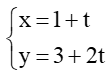 và d2: x – 3y + 2 = 0;
và d2: x – 3y + 2 = 0;
c) 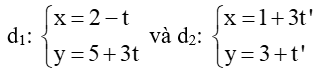
Trả lời
a) Gọi A là giao điểm của đường thẳng d1 và d2. Khi đó tọa độ điểm A là nghiệm của hệ phương trình:
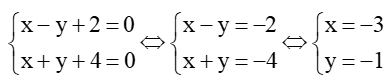
⇒ A(-3; -1).
Ta có:
Đường thẳng d1: x – y + 2 = 0 có VTPT là →n1(1; -1);
Đường thẳng d2: x + y + 4 = 0 có VTPT là →n2(1; 1);
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
cos(d1; d2) = 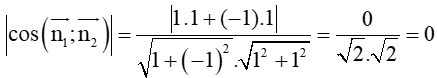
⇒ (d1; d2) = 90°
Vậy giao điểm của hai đường thẳng d1 và d2 là A(-3; -1) và góc giữa hai đường thẳng d1 và d2 là 90°.
b) Ta có: d1: 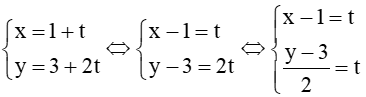
⇔ x – 1 = y−32
⇔ 2x – 2 = y – 3
⇔ 2x – y + 1 = 0
Gọi B là giao điểm của đường thẳng d1 và d2. Khi đó tọa độ điểm B là nghiệm của hệ phương trình:
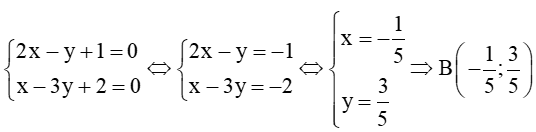
Ta có:
Đường thẳng d1: 2x – y + 1 = 0 có VTPT là →n1(2; -1);
Đường thẳng d2: x – 3y + 2 = 0 có VTPT là →n2(1; -3);
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
cos(d1; d2) = 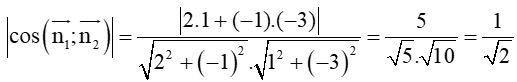
⇒ (d1; d2) = 45°
Vậy giao điểm của hai đường thẳng d1 và d2 là B(−15;35) và góc giữa hai đường thẳng d1 và d2 là 45°.
c) Gọi C là giao điểm của đường thẳng d1 và d2. Khi đó tọa độ điểm C là nghiệm của hệ phương trình:
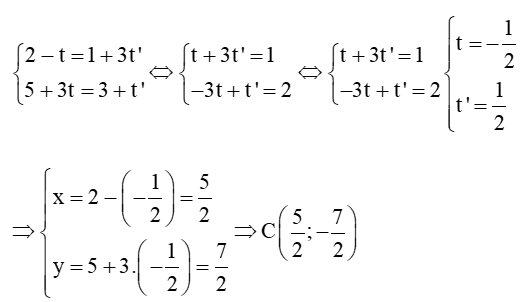
Ta có:
Đường thẳng d1: 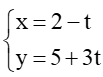 có VTCP là →u1 = (-1; 3);
có VTCP là →u1 = (-1; 3);
Đường thẳng d2: 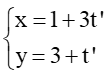 có VTCP là →u2 = (3; 1).
có VTCP là →u2 = (3; 1).
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
cos(d1; d2) = 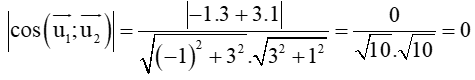
⇒ (d1; d2) = 90°
Vậy giao điểm của hai đường thẳng d1 và d2 là C(52;72) và góc giữa hai đường thẳng d1 và d2 bằng 90°.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài tập cuối chương 9
Bài 1: Không gian mẫu và biến cố
Bài 2: Xác suất của biến cố
Bài tập cuối chương 10
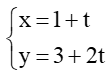

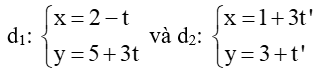
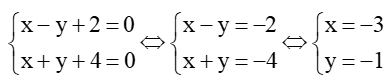
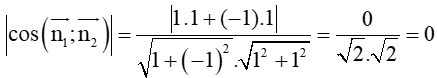
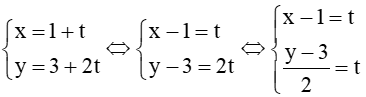
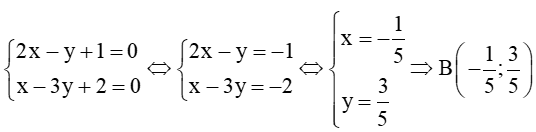
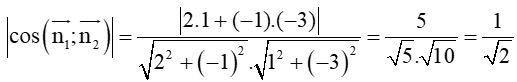
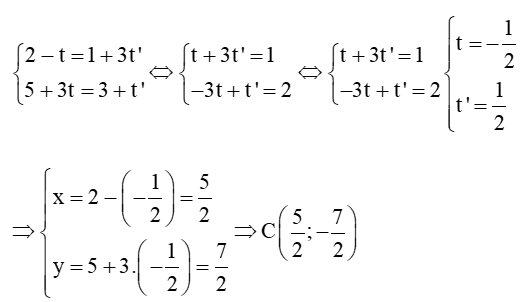
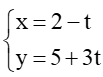 có VTCP là
có VTCP là 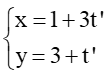 có VTCP là
có VTCP là