Tìm tất cả các giá trị thực của tham số m để phương trình \({4^x} - {2^{x + 3}} + 3 = m\) có đúng 2 nghiệm thực phân biệt trong khoảng \(\left( {1;3} \right)\).
D. \(3 < m < 9\)
Đáp án A
Phương pháp:
Đặt \({2^x} = t,\,\,t \in \left( {2;8} \right)\). Khảo sát hàm số \(y = f\left( t \right) = {t^2} - 8t + 3\) với \(t \in \left( {2;8} \right)\), từ đó đưa ra kết luận.
Cách giải:
Ta có: \({4^x} - {2^{x + 3}} + 3 = m\,\,\,\left( 1 \right)\)
Đặt \({2^x} = t,\,\,t \in \left( {2;8} \right)\). Phương trình (1) trở thành \({t^2} - 8t + 3 = m\,\,\,\left( 2 \right)\), với \(t \in \left( {2;8} \right)\)
Nhận xét: Ứng với mỗi giá trị t tìm được thuộc khoảng \(\left( {2;8} \right)\) ta tìm được đúng một giá trị x thuộc khoảng \(\left( {1;3} \right)\), nên để phương trình (1) có đúng 2 nghiệm phân biệt trong khoảng \(\left( {1;3} \right)\) thì phương trình (2) có đúng 2 nghiệm phân biệt trong khoảng \(\left( {2;8} \right)\).
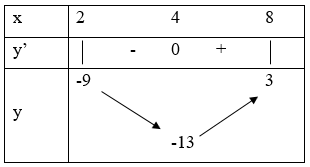
Xét hàm số \(y = f\left( t \right) = {t^2} - 8t + 3\) với \(t \in \left( {2;8} \right)\)
\(y' = f'\left( t \right) = 2t - 8,\,\,\,y' = 0 \Leftrightarrow t = 4\)
Bảng biến thiên:
Để phương trình (2) có 2 nghiệm phân biệt thuộc \(\left( {2;8} \right)\) thì \(m \in \left( { - 13;9} \right)\)
Kết luận: \( - 13 < m < - 9\)