Tìm tất cả các giá trị của tham số m để đồ thị hàm số y= x^3 - 3x^2 - m cắt trục hoành tại đúng một điểm. A. m thuộc ( - vô cùng; 0] [ 2; + vô cùng). B. m thuộc ( - vô cùng; - 4) ( 0; + vô
60
26/04/2024
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y=x3−3x2−m cắt trục hoành tại đúng một điểm.
A. m∈(−∞;0]∪[2;+∞).
B. m∈(−∞;−4)∪(0;+∞).
C. m∈(−∞;−4]∪[0;+∞).
D. m∈(−∞;0)∪(2;+∞).
Trả lời
Lời giải
Xét phương trình hoành độ giao điểm của đồ thị hàm số y=x3−3x2−m và trục hoành:
x3−3x2−m=0⇔x3−3x2=m (*)
Xét hàm số f(x)=x3−3x2 có tập xác định D=R.
Ta có: f′(x)=3x2−6x.
f′(x)=0⇔3x2−6x=0⇔[x=0⇒f(0)=0x=2⇒f(2)=−4.
lim; \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} - 3{x^2}} \right) = + \infty .
Bảng biến thiên:
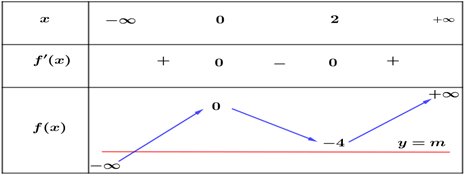
Đồ thị hàm số y = {x^3} - 3{x^2} - m cắt trục hoành tại đúng một điểm \Leftrightarrow Phương trình (*) có đúng một nghiệm.
Do đó từ bảng biến thiên ta được: yêu cầu bài toán \Leftrightarrow \left[ \begin{array}{l}m < - 4\\m > 0\end{array} \right..

