Tìm m để giá trị nhỏ nhất của hàm số y = x^3 - 3x^2 - 9x + m trên đoạn [ 0;4] bằng - 25, khi đó hãy tính giá trị của biểu thức P = 2m + 1 A. 7 B. 5 C. 3 D. 1
79
05/05/2024
Tìm \(m\) để giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + m\) trên đoạn \(\left[ {0;4} \right]\) bằng \( - 25\), khi đó hãy tính giá trị của biểu thức \(P = 2m + 1\).
A. \(7\).
B. \(5\).
C. \(3\).
D. \(1\).
Trả lời
Lời giải
Chọn B
Xét hàm số \(y = {x^3} - 3{x^2} - 9x + m\) trên đoạn \(\left[ {0;4} \right]\).
Ta có \(y' = 3{{\rm{x}}^2} - 6{\rm{x}} - 9\), \(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 3}\end{array}} \right.\).
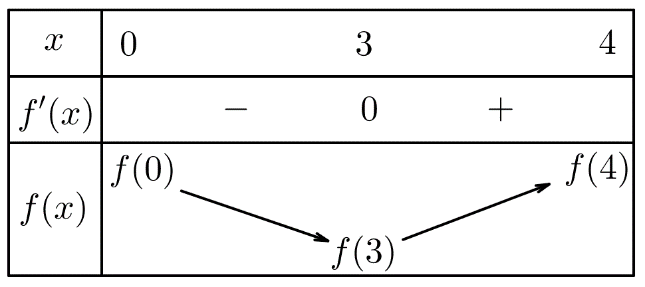
Từ bảng biến thiên suy ra \(\mathop {{\rm{min}}}\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( 3 \right)\) \( \Leftrightarrow f\left( 3 \right) = - 25 \Leftrightarrow m - 27 = - 25 \Leftrightarrow m = 2\).
Suy ra \(P = 2m + 1 = 5\).

