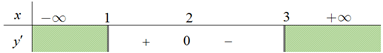Tìm khoảng nghịch biến của hàm số y = căn bậc hai của 3 - x + căn bậc hai của x - 1. A. ( 1;3). B. ( - vô cùng ;2) . C. ( 2; 3). D. ( 2; + vô cùng).
Tìm khoảng nghịch biến của hàm số y=√3−x+√x−1.
A. (1;3).
B. (−∞;2) .
C. (2;3).
D. (2;+∞).
Lời giải
Tập xác định: D=[1;3].
Ta có y′=12√x−1−12√3−x.
y′=0⇔12√x−1−12√3−x=0⇔x−1=3−x⇔x=2.
y′ không xác định khi [√x−1=0√3−x=0⇔[x=1x=3.
Bảng xét dấu đạo hàm
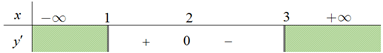
Dựa vào bảng xét dấu của đạo hàm, ta thấy hàm số đã cho nghịch biến trên (2;3).