Tìm giá trị nhỏ nhất của hàm số y = x - 5 + 1/x trên khoảng ( 0; + vô cùng). A. ( 0; + vô cùng) y = 2. B. ( 0; + vô cùng) y = - 4
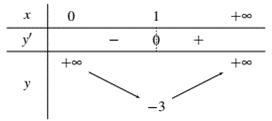
Tìm giá trị nhỏ nhất của hàm số \(y = x - 5 + \frac{1}{x}\) trên khoảng \(\left( {0; + \infty } \right)\).
A. \[\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = 2\].
B. \[\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = - 4\].
C. \[\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = - 3\].
D. \[\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = - 5\].