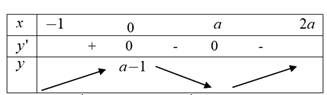
Tìm a để giá trị lớn nhất của hàm số y = x^3 - 3ax^2 + a - 1 trên đoạn [ - 1;a] bằng 10, biết a > 0 A. a = 10 B. a = 11 C. a = 5/2 D. a = 3/2

59 01/05/2024

Tìm

$a$ để giá trị lớn nhất của hàm số

$y = {x^3} - 3a{x^2} + a - 1$ trên đoạn

$\left[ { - 1;a} \right]$ bằng 10, biết

$a > 0$ .

$a = 10$ .

$a = 11$ .

$a = \frac{5}{2}$ .

$a = \frac{3}{2}$ .

Trả lời

Lời giải

Chọn B

Ta có $y' = 3{x^2} - 6ax = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2a\end{array} \right.$

Khi đó bảng biến thiên của hàm số trên đoạn $\left[ { - 1;a} \right]$

Media VietJack

Từ bảng biến thiên của hàm số ta được

$\mathop {\max }\limits_{\left[ { - 1;a} \right]} y = 10 = y(0) = a - 1 \Rightarrow a = 11.$

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

Câu hỏi cùng chủ đề

Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình bên. Hàm số g( x ) = f( x^2 + 2x) - x^2 - 2x đồng biến trên khoảng nào dưới đây? A. ( - 1 - căn bậc hai của 2 ; - 1).

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

114 11 tháng trước

Cho hàm số y = f( x ) có bảng biến thiên như sau Số nghiệm thuộc [ 0; 3pi /2] của phương trình | f( cos 2x)| = 1 là A. 9 B. 4 C. 7 D. 10

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

98 11 tháng trước

Cho hàm số y = f( x ) xác định, liên tục trên R và có đúng hai điểm cực trị x = - 1,x = 1, có đồ thị như hình vẽ sau: Hỏi hàm số y = f( x^2 - 2x + 1) + 2020 có bao nhiêu điểm cực tiểu?

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

129 11 tháng trước

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( ABC), BC = a, góc hợp bởi (SBC) và ( ABC) là 60^0. Mặt phẳng ( P )qua A vuông góc với SC cắt SB,SC lần l

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

95 11 tháng trước

Số điểm cực trị của hàm số f( x ) có đạo hàm f'( x ) = ( x + 1)( x - 2)^2, x thuộc R là A. 0 B. 3 C. 1 D. 2

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

91 11 tháng trước

Đường cong ở hình vẽ dưới đây là đồ thị của hàm số y = ax + b/cx + d với (a,b,c,d) là các số thực. Mệnh đề nào dưới đây đúng ? A. y' < 0, x khác - 1. B. y' > 0, x thuộc R C. y' > 0, x

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

90 11 tháng trước

Cho hàm số y = căn bậc hai của x^2 - 2x - 3. Khẳng định nào sau đây là đúng? A. maxy = 1 B. maxy = 2 C. maxy = 0 D. Hàm số không có giá trị lớn nhất.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

109 11 tháng trước

Cho hàm số bậc ba y = f( x ) có đồ thị như hình vẽ: Khi đó phương trình 2f( x) - 1 = 0 có bao nhiêu nghiệm thực phân biệt. A. 3. B. 0 C. 1. D. 2.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

120 11 tháng trước

Tìm tất cả các giá trị thực của tham số m để hàm số y = - 1/3x^3 - mx^2 + ( 2m - 3)x + 2018 nghịch biến trên R A. - 3 nhỏ hơn bằng m nhỏ hơn bằng 1 B. - 3 < m < 1 C. m lớn hơn b

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

133 11 tháng trước

Biết đồ thị hàm số y = f( x ) có một tiệm cận ngang là y = 3. Khi đó đồ thị hàm số y = 2f( x ) - 4 có một tiệm cận ngang là A. y = 3 B. y = 2 C. y = 1 D. y = - 4

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

111 11 tháng trước

Xem tất cả

Tìm a để giá trị lớn nhất của hàm số y = x^3 - 3ax^2 + a - 1 trên đoạn [ - 1;a] bằng 10, biết a > 0 A. a = 10 B. a = 11 C. a = 5/2 D. a = 3/2

Trả lời

Câu hỏi cùng chủ đề

Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình bên. Hàm số g( x ) = f( x^2 + 2x) - x^2 - 2x đồng biến trên khoảng nào dưới đây? A. ( - 1 - căn bậc hai của 2 ; - 1).

Cho hàm số y = f( x ) có bảng biến thiên như sau Số nghiệm thuộc [ 0; 3pi /2] của phương trình | f( cos 2x)| = 1 là A. 9 B. 4 C. 7 D. 10

Cho hàm số y = f( x ) xác định, liên tục trên R và có đúng hai điểm cực trị x = - 1,x = 1, có đồ thị như hình vẽ sau: Hỏi hàm số y = f( x^2 - 2x + 1) + 2020 có bao nhiêu điểm cực tiểu?

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( ABC), BC = a, góc hợp bởi (SBC) và ( ABC) là 60^0. Mặt phẳng ( P )qua A vuông góc với SC cắt SB,SC lần l

Số điểm cực trị của hàm số f( x ) có đạo hàm f'( x ) = ( x + 1)( x - 2)^2, x thuộc R là A. 0 B. 3 C. 1 D. 2

Đường cong ở hình vẽ dưới đây là đồ thị của hàm số y = ax + b/cx + d với (a,b,c,d) là các số thực. Mệnh đề nào dưới đây đúng ? A. y' < 0, x khác - 1. B. y' > 0, x thuộc R C. y' > 0, x

Cho hàm số y = căn bậc hai của x^2 - 2x - 3. Khẳng định nào sau đây là đúng? A. maxy = 1 B. maxy = 2 C. maxy = 0 D. Hàm số không có giá trị lớn nhất.

Cho hàm số bậc ba y = f( x ) có đồ thị như hình vẽ: Khi đó phương trình 2f( x) - 1 = 0 có bao nhiêu nghiệm thực phân biệt. A. 3. B. 0 C. 1. D. 2.

Tìm tất cả các giá trị thực của tham số m để hàm số y = - 1/3x^3 - mx^2 + ( 2m - 3)x + 2018 nghịch biến trên R A. - 3 nhỏ hơn bằng m nhỏ hơn bằng 1 B. - 3 < m < 1 C. m lớn hơn b

Biết đồ thị hàm số y = f( x ) có một tiệm cận ngang là y = 3. Khi đó đồ thị hàm số y = 2f( x ) - 4 có một tiệm cận ngang là A. y = 3 B. y = 2 C. y = 1 D. y = - 4

Danh mục