Thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC = 2a là A. 8x^3 / 3 căn bậc hai 3
Thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC=2a là
A. 8a33√3
B. 2a3√2
C. 3a3√3
D. 8a327
Thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC=2a là
D. 8a327
Đáp án B
Phương pháp:
Thể tích khối lập phương có các cạnh đều bằng a là: V=a3
Cách giải:
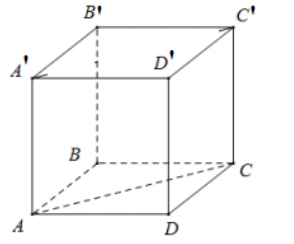
ABCD là hình vuông ⇒AC=√2AB⇔2a=√2AB⇔AB=√2a
⇒ Khối lập phương ABCD.A’B’C’D’ có các cạnh đều bằng √2a
Thể tích khối lập phương đó là: V=(√2a)3=2√3a3