Thể tích của khối lăng trụ đều ABC.A’B’C’ biết cạnh đáy \[AB = a\], góc giữa A’B và mặt bên (ACC’A’) bằng \({45^0}\)

D. \(V = \frac{{{a^3}\sqrt 6 }}{{24}}\)

Đáp án A

Phương pháp:

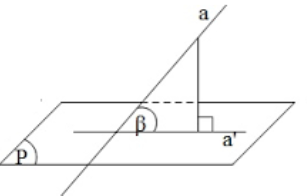
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).

Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.

Cách giải:

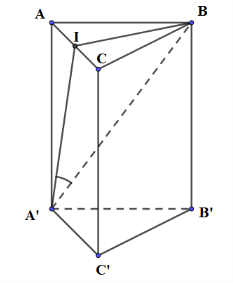
Gọi I là trung điểm của AC. \(\Delta ABC\) đều, \(AB = a \Rightarrow B = \frac{{a\sqrt 3 }}{2},\,\,\,{S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\) và \(BI \bot AC\)

Mà \(BI \bot AA'\left( {do\,AA' \bot \left( {ABC} \right)} \right)\)

\( \Rightarrow BI \bot \left( {ACC'A'} \right) \Rightarrow \left( {A'B;\left( {ACC'A'} \right)} \right) = \left( {A'B;A'I} \right) = IA'B = {45^0}\)

\(\Delta IA'B\) vuông tại I, \(IA'B = {45^0} \Rightarrow \Delta IA'B\) vuông cân tại I

\( \Rightarrow A'B = \sqrt 2 .IB = \sqrt 2 .\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{2}\)

\(\Delta ABA'\) vuông tại A \( \Rightarrow AA' = \sqrt {A'{B^2} - A{B^2}} = \sqrt {\left( {\frac{{a\sqrt 6 }}{2}} \right) - {a^2}} = \frac{{a\sqrt 2 }}{2}\)

Thể tích khối lăng trụ đều ABC.A’B’C’ là: \(V = {S_{ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 6 }}{8}\)