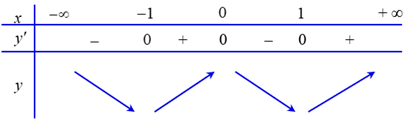
Số điểm cực tiểu của hàm số y = x^4 - 2x^2 + 2 là A. 0 B. 2 C. 1 D. 3
Số điểm cực tiểu của hàm số \(y = {x^4} - 2{x^2} + 2\) là
A. \(0\).
B. \(2\).
C. \(1\).
D. \(3\).
Lời giải
Cách 1:
Tập xác định \(D = \mathbb{R}\).
Ta thấy, hàm số \(y = {x^4} - 2{x^2} + 2\) có \(a = 1 > 0\) và \(b = - 2 < 0\) nên hàm số có \(2\) điểm cực tiểu.
Cách 2:
Tập xác định: \(D = \mathbb{R}\).
Đạo hàm: \(y' = 4{x^3} - 4x\).
\(y' = 0\)\( \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\).
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy, hàm số có \(2\) điểm cực tiểu là \(x = - 1\) và \(x = 1\).