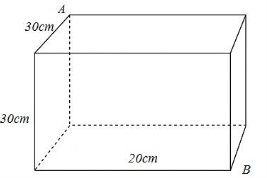
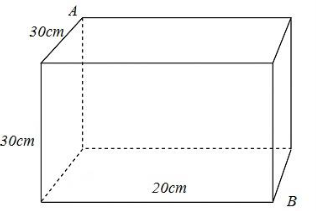
Một khối gỗ hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là 30cm, 20cm và 30cm (như hình vẽ). Một con kiến xuất phát từ điểm A muốn tới điểm B thì quãng đường ngắn nhất nó phải đi là bao nhiêu cm?
B. \(10\sqrt {34} \,cm\)
D. \(20 + 30\sqrt 2 \,cm\)
Đáp án B
Phương pháp:
Trải tất cả các mặt của hình hộp chữ nhật ra cùng một mặt phẳng.
Cách giải:
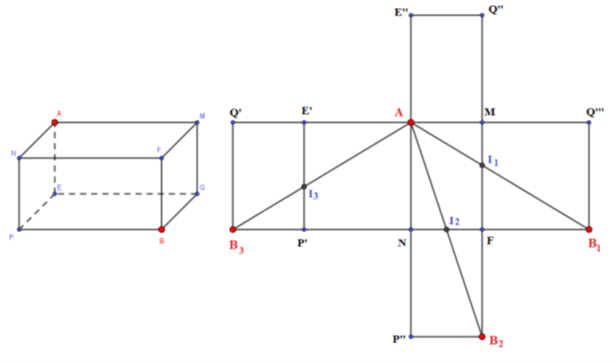
Để đến được B, đầu tiên con kiến phải đi trên một trong các mặt bên và đi đến một trong các cạnh bên: NP, PE, QE, MQ, MF, NF
* Giả sử con kiến đi đến I trên cạnh MF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài \(AB = \sqrt {A{Q^2} + Q{B^2}} = \sqrt {{{50}^2} + {{30}^2}} = 10\sqrt {34} \left( {cm} \right)\)
* Giả sử con kiến đi đến I trên cạnh NF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài \(AB = \sqrt {A{P^2} + P{B^2}} = \sqrt {{{60}^2} + {{20}^2}} = 20\sqrt {10} \left( {cm} \right)\)
* Giả sử con kiến đi đến I trên cạnh PF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài \(AB = \sqrt {A{N^2} + N{B^2}} = \sqrt {{{30}^2} + {{50}^2}} = 10\sqrt {34} \left( {cm} \right)\)
Vậy, quãng đường ngắn nhất con kiến đi là \(10\sqrt {34} \left( {cm} \right)\)