Một chất điểm chuyển động theo quy luật S = - 1/3t^3 + 4t^2 + 9t với (t) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và (S) (mét) là quãng đường vật chuyển động trong thời
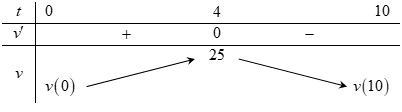
Một chất điểm chuyển động theo quy luật \(S = - \frac{1}{3}{t^3} + 4{t^2} + 9t\) với \(t\) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \(S\) (mét) là quãng đường vật chuyển động trong thời gian đó. Hỏi trong khoảng thời gian \(10\) giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của chất điểm là bao nhiêu?
A. \(88\left( {{\rm{m/s}}} \right).\)
B. \(25\left( {{\rm{m/s}}} \right).\)
C. \(100\left( {{\rm{m/s}}} \right).\)
D. \(11\left( {{\rm{m/s}}} \right).\)