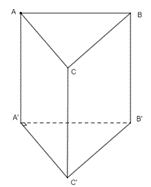
Lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông tại A, BC = 2a, AB = a. Mặt bên (BB'C'C) là hình vuông. Khi đó thể tích lăng trụ là A. a^3 căn bậc hai của 2 B. a^3 căn bậc hai của 3
Lăng trụ đứng \[ABCA'B'C'\] có đáy \[ABC\] là tam giác vuông tại \[A\], \[BC = 2a,{\rm{ }}AB = a\]. Mặt bên \[(BB'C'C)\] là hình vuông. Khi đó thể tích lăng trụ là
A. \[{a^3}\sqrt 2 \].
B. \[{a^3}\sqrt 3 \].
C. \[2{a^3}\sqrt 3 \].
D. \[\frac{{{a^3}\sqrt 3 }}{3}\].
