Khối lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó thể tích khối chóp D.ABC'D' bằng A. a^3 căn bậc hai của 2 /3 B. a^3/3 C. a^3/4. D. a^3 căn bậc hai của 2 /6
74
06/05/2024
Khối lập phương \(ABCD.A'B'C'D'\)có cạnh bằng \(a.\) Khi đó thể tích khối chóp \(D.ABC'D'\) bằng
A. \(\frac{{{a^3}\sqrt 2 }}{3}\).
B. \(\frac{{{a^3}}}{3}\).
C. \(\frac{{{a^3}}}{4}\).
D. \(\frac{{{a^3}\sqrt 2 }}{6}\).
Trả lời
Lời giải
Chọn B
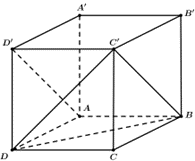
Ta có: \[{V_{ABCD.A'B'C'D'}} = {V_{A'AD'.B'BC'}} + {V_{D.ABC'D'}} + {V_{C'.BCD}}.\]
Ta lại có:
\[{V_{ABCD.A'B'C'D'}} = {a^3}\].
\[{V_{C'.BCD}} = \frac{1}{3}{S_{BCD}}.CC' = \frac{1}{3}\frac{{{a^2}}}{2}.a = \frac{{{a^3}}}{6}.\]
\[{V_{A'AD'.B'BC'}} = {S_{AA'D}}.A'B' = \frac{1}{2}{a^2}.a = \frac{1}{2}{a^3}.\]
Suy ra: \[{V_{D.ABC'D'}} = {V_{ABCD.A'B'C'D'}} - {V_{A'AD'.B'BC'}} - {V_{C'.BCD}} = {a^3} - \frac{{{a^3}}}{6} - \frac{{{a^3}}}{2} = \frac{{{a^3}}}{3}\]

