Hình chóp tứ giác đều nội tiếp mặt cầu bán kính\(R = 9\), có chiều cao \(h = \frac{{4R}}{3}\), thể tích của khối chóp đó là V.

D. \(V = 576\)

Đáp án D

Phương pháp:

Thể tích khối chóp \(V = \frac{1}{3}Sh\)

Cách giải:

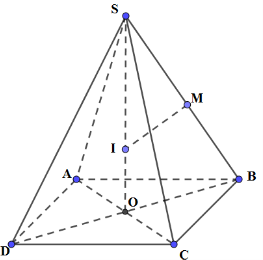
Gọi O là tâm của hình vuông ABCD; M là trung điểm của SB; I là giao điểm của SO với mặt phẳng trung trực của đoạn SB. Khi đó, I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.

Theo đề bài, ta có: \(\left\{ \begin{array}{l}IS = IA = IB = IC = ID = R = 9\\SO = h = \frac{{4R}}{3} = \frac{{4.9}}{3} = 12\end{array} \right.\)

\(\Delta SIM\) đồng dạng

\( \Leftrightarrow S{O^2} + O{B^2} = 2SI.SO \Leftrightarrow {12^2} + O{B^2} = 2.9.12 \Leftrightarrow O{B^2} = 72 \Rightarrow OB = 6\sqrt 2 \)

\( \Rightarrow AB = \sqrt 2 .OB = \sqrt 2 .6 = 12 \Rightarrow {S_{ABCD}} = {12^2} = 144\)

Thể tích khối chóp \({V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SO = \frac{1}{3}.144.12 = 576\)