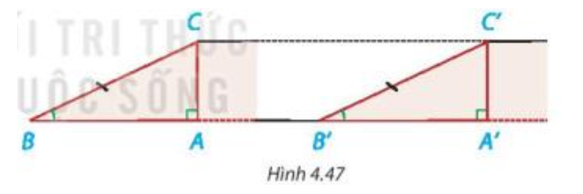
Hình 4.47 mô phỏng chiều dài và độ dốc của hai con dốc bởi các đường thẳng BC, B'C' và các góc B, B'

HĐ 3 trang 76 Toán 7 Tập 1: Hình 4.47 mô phỏng chiều dài và độ dốc của hai con dốc bởi các đường thẳng BC, B'C' và các góc B, B'. Khi đó AC, A'C' mô tả độ cao của hai con dốc.

a) Dựa vào trường hợp bằng nhau góc – cạnh – góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A’B’C’  bằng nhau.

b) So sánh độ cao của hai con dốc.

Trả lời

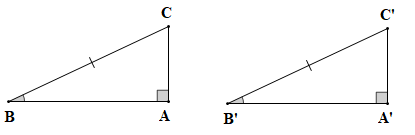
Hình ảnh hai con dốc trong đề bài được mô tả bởi hình vẽ dưới đây:

+) Tam giác ABC vuông tại A nên hai góc nhọn của tam giác phụ nhau.

Do đó $\widehat{B}+\widehat{C}=90°.$ Suy ra $\widehat{C}=90°-\widehat{B}.$ 

Tam giác A'B'C' vuông tại A' nên hai góc nhọn của tam giác phụ nhau.

Do đó $\widehat{B^{\text{'}}}+\widehat{C^{\text{'}}}=90°.$ Suy ra $\widehat{C^{\text{'}}}=90°-\widehat{B^{\text{'}}}.$ 

Mà $\widehat{B}=\widehat{B^{\text{'}}}$ (theo giả thiết).

Do đó $90°-\widehat{B}=90°-\widehat{B^{\text{'}}}$.

Suy ra $\widehat{C}=\widehat{C^{\text{'}}}.$ 

Xét tam giác ABC và tam giác A'B'C' có:

$\widehat{B}=\widehat{B^{\text{'}}}$ (theo giả thiết);

BC = B'C' (theo giả thiết);

$\widehat{C}=\widehat{C^{\text{'}}}$ (chứng minh trên).

Vậy $\Delta ABC=\Delta A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ (g.c.g).

b) Từ $\Delta ABC=\Delta A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}$ (chứng minh câu a) suy ra AC = A'C' (hai cạnh tương ứng).

Vậy độ cao của hai con dốc đó bằng nhau.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Luyện tập chung trang 74

Bài 15: Các trường hợp bằng nhau của tam giác vuông

Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Luyện tập chung trang 86

Bài tập cuối chương 4 trang 87