Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Video giải bài tập Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Mở đầu
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Ngoài cách sử dụng trường hợp bằng nhau cạnh – cạnh – cạnh để khẳng định hai tam giác bằng nhau thì có thể sử dụng hai trường hợp bằng nhau khác để khẳng định hai tam giác bằng nhau.
Trường hợp bằng nhau cạnh – góc – cạnh (c.g.c): Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Trường hợp bằng nhau góc – cạnh – góc (g.c.g): Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
1. Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c)
Giải Toán 7 trang 70 Tập 1
Nối điểm B với điểm C ta được tam giác ABC (H.4.27).
Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.
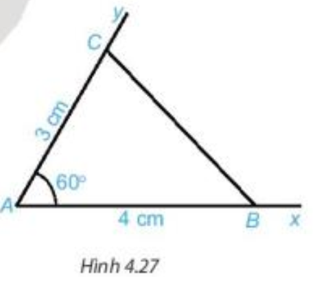
Lời giải:
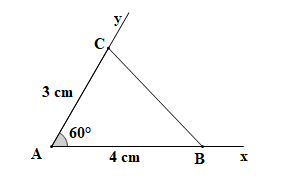
Dùng thước thẳng có vạch chia đo độ dài cạnh BC ta được kết quả BC = 3,6 cm.
HĐ 2 trang 70 Toán 7 Tập 1: Vẽ thêm tam giác A'B'C' với A'B' = 4 cm và A'C' = 3 cm (H.4.28).
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và A'B'C'.
- Hai tam giác ABC và A'B'C' có bằng nhau không?
- Độ dài các cạnh BC và B'C' của hai tam giác em vừa vẽ có bằng các cạnh AB và A'B' của hai tam giác các bạn khác vẽ không?
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
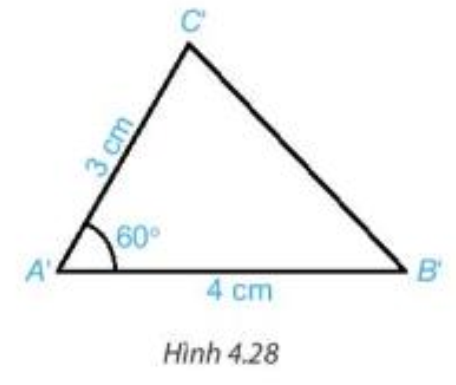
Lời giải:
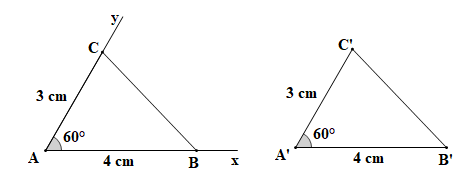
+) Sau khi dùng thước thẳng có vạch chia (hoặc compa) ta thấy hai tam giác ABC và A'B'C' có: AB = A'B', BC = B'C', AC = A'C'.
Do đó (c.c.c).
+) Độ dài các cạnh BC và B'C' của hai tam giác em vẽ bằng các cạnh BC và B'C' của hai tam giác các bạn khác vẽ.
+) Hai tam giác em vừa vẽ bằng hai tam giác các bạn khác vẽ.
Giải Toán 7 trang 71 Tập 1
Câu hỏi trang 71 Toán 7 Tập 1: Trong Hình 4.29, hai tam giác nào bằng nhau?
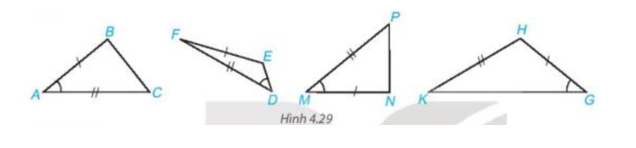
Lời giải:
Hai tam giác ABC và tam giác MNP có:
AB = MN, AC = MP (với lần lượt là góc xen giữa hai cạnh tương ứng bằng nhau của mỗi tam giác).
Do đó (c.g.c).
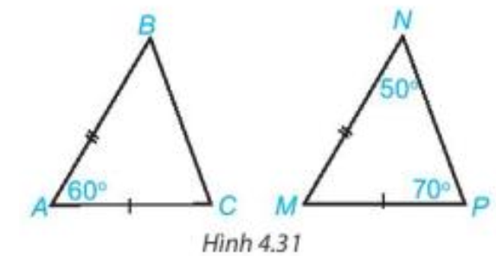
Lời giải:
|
GT |
AB = MN, AC = MP;
|
|
KL |
Hai tam giác ABC và MNP có bằng nhau không? |
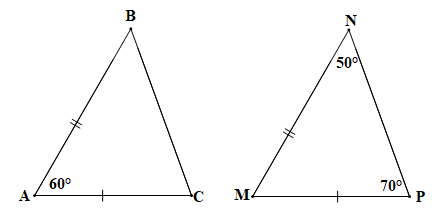
Chứng minh (hình vẽ trên):
Áp dụng định lí tổng ba góc trong một tam giác cho tam giác MNP ta có:
Suy ra
Do đó
Xét hai tam giác ABC và MNP có:
AB = MN (theo giả thiết);
(chứng minh trên);
AC = MP (theo giả thiết).
Vậy (c.g.c).
Vận dụng trang 71 Toán 7 Tập 1: Cho Hình 4.32, biết OA = OD và AB = CD. Chứng minh rằng:
a) AC = DB;
b)
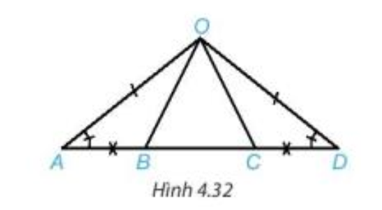
Lời giải:
|
GT |
OA = OD, AB = CD. |
|
KL |
a) AC = DB; b) |
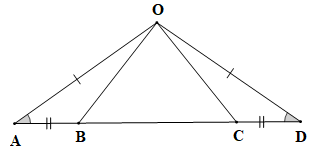
Chứng minh (hình vẽ trên):
a) Ta có: AC = AB + BC; BD = BC + CD.
Mà AB = CD (theo giả thiết), do đó AC = DB.
b) Xét tam giác OAC và tam giác ODB có:
OA = OD (theo giả thiết);
(do (theo giả thiết));
AC = DB (chứng minh câu a).
Vậy (c.g.c).
2. Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g.c.g)
Giải Toán 7 trang 72 Tập 1
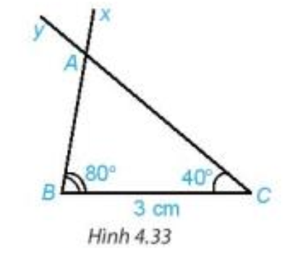
HĐ 3 trang 72 Toán 7 Tập 1: Vẽ đoạn thẳng BC = 3 cm. Vẽ hai tia Bx và Cy sao cho như Hình 4.33.
Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC (H.4.33).
Dùng thước thẳng có vạch chia đo độ dài hai cạnh AB, AC của tam giác ABC.
Lời giải:
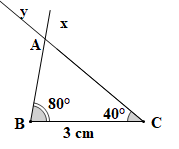
Dùng thước thẳng có vạch chia đo độ dài cạnh AB và AC ta được:
AB = 2,2 cm; AC = 3,4 cm.
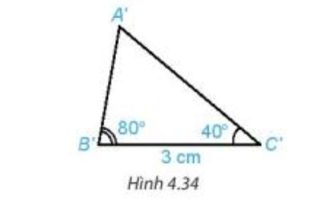
HĐ 4 trang 72 Toán 7 Tập 1: Vẽ thêm tam giác sao cho B'C' = 3 cm, (H.4.34).
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác ABC và A'B'C'. Hai tam giác ABC và A'B'C' có bằng nhau không?
Lời giải:
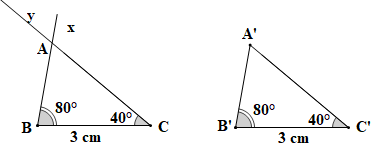
Dùng thước thẳng có vạch chia ta đo độ dài cạnh A'B' và A'C' được:
A'B' = 2,2 cm, A'C' = 3,4 cm.
Do đó AB = A'B'; AC = A'C'; BC = B'C'.
Vậy (c.c.c).
Câu hỏi trang 72 Toán 7 Tập 1: Hai tam giác nào trong Hình 4.35 bằng nhau?
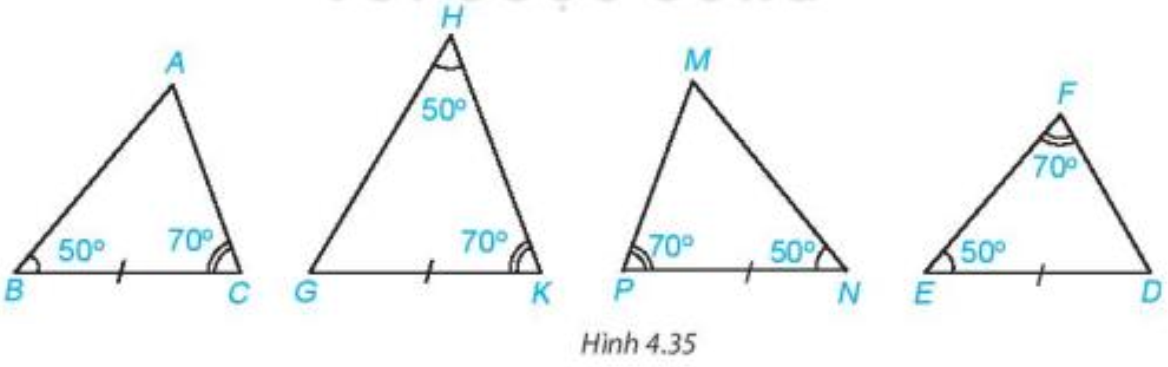
Lời giải:
Xét tam giác ABC và tam giác MNP có:
BC = NP;
Vậy (g.c.g).
Các tam giác còn lại tuy có các góc bằng nhau nhưng các cạnh bằng nhau lại không phải cạnh xen giữa các góc.
Giải Toán 7 trang 73 Tập 1
Luyện tập 2 trang 73 Toán 7 Tập 1: Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau.
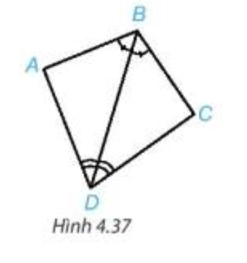
Lời giải:
|
GT |
|
|
KL |
|
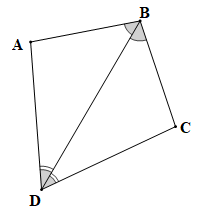 Chứng minh (hình vẽ trên):
Chứng minh (hình vẽ trên):
Xét tam giác ABD và tam giác CBD có:
(theo giả thiết);
DB là cạnh chung;
(theo giả thiết).
Vậy (g.c.g).
Thử thách nhỏ trang 73 Toán 7 Tập 1: Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?
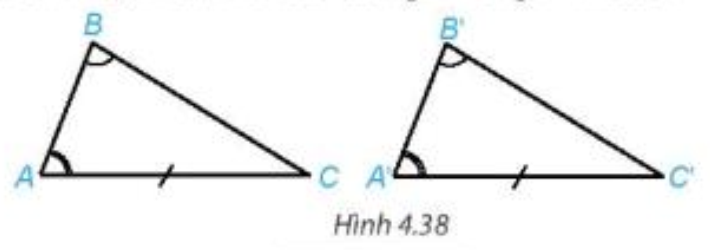
Lời giải:
|
GT |
AC = A'C'. |
|
KL |
và có bằng nhau không? |
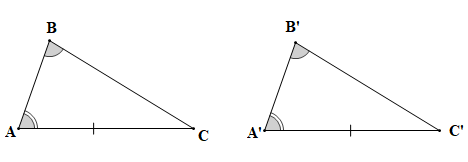
Chứng minh (hình vẽ trên):
Áp dụng định lí tổng ba góc trong một tam giác cho tam giác ABC và tam giác A'B'C' ta có:
Trong tam giác ABC: , suy ra
Trong tam giác A'B'C': ,
Suy ra
Mà (theo giả thiết).
Do đó .
Nên
Hay
Xét tam giác ABC và tam giác A'B'C' có:
(theo giả thiết);
AC = A'C' (theo giả thiết);
(chứng minh trên).
Vậy (g.c.g).
Vậy bạn Lan nói đúng.
Bài tập
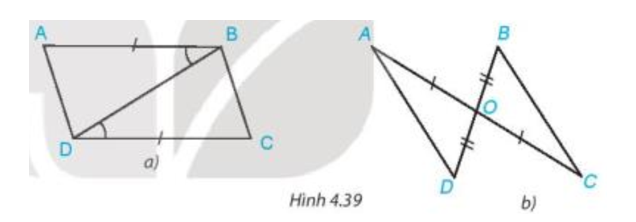
Lời giải:
+) Hình 4.39 a)
|
GT |
AB = CD. |
|
KL |
Chỉ ra một cặp tam giác bằng nhau. Giải thích vì sao chúng bằng nhau. |
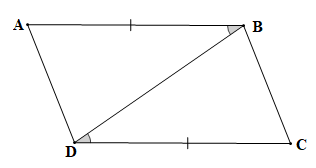
Xét tam giác ABD và tam giác CDB có:
AB = CD (theo giả thiết);
(theo giả thiết);
BD là cạnh chung.
Vậy (c.g.c).
+) Hình 4.39 b)
|
GT |
OA = OC, OD = OB. |
|
KL |
Chỉ ra một cặp tam giác bằng nhau. Giải thích vì sao chúng bằng nhau. |
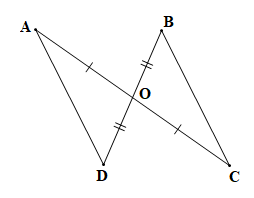
Xét tam giác OAD và tam giác OCB có:
OA = OC (theo giả thiết);
(hai góc đối đỉnh);
OD = OB (theo giả thiết).
Vậy (c.g.c).
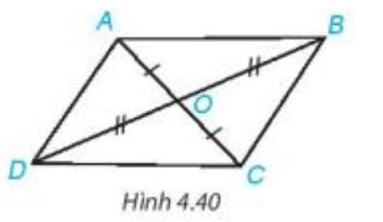
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.
b) Chứng minh rằng
Lời giải:
|
GT |
OA = OC, OB = OD. |
|
KL |
a) Tìm hai cặp tam giác có chung đỉnh O bằng nhau; b) Chứng minh |
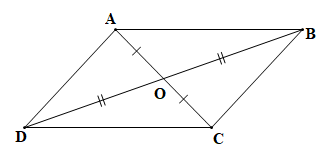
a) Hai cặp tam giác có chung đỉnh O bằng nhau là:
+) Tam giác OAB và tam giác OCD
Giải thích:
OA = OC (giải thuyết)
OB = OD (giải thuyết)
(hai góc đối đỉnh)
Do đó, (c – g – c)
+) Tam giác OAD và tam giác OCB.
Giải thích:
OA = OC (giải thuyết)
OD = OB (giải thuyết)
(hai góc đối đỉnh)
Do đó, (c – g – c)
b) (Chứng minh ở câu a) nên (hai góc tương ứng) hay
(Chứng minh ở câu a) nên (hai góc tương ứng) hay
+) Xét tam giác DAB và tam giác BCD có:
(chứng minh trên);
BD là cạnh chung;
(chứng minh trên).
Vậy (g.c.g).
Bài 4.14 trang 73 Toán 7 Tập 1: Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
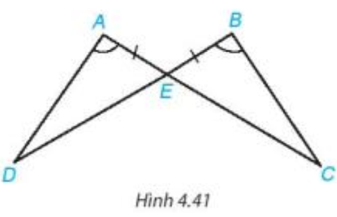
Lời giải:
|
GT |
AE = BE, |
|
KL |
|
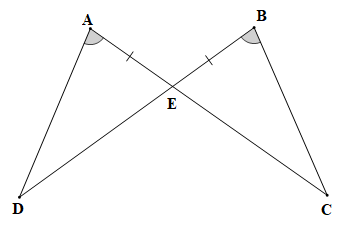
Chứng minh (hình vẽ trên):
Xét tam giác ADE và tam giác BCE có:
(theo giả thiết);
AE = BE (theo giả thiết);
(hai góc đối đỉnh).
Vậy (g.c.g).
a)
b) EG = EH.
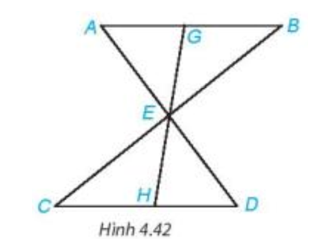
Lời giải:
|
GT |
AB = CD, AB // CD; E là giao điểm của AD và BC; ; G, E, H thẳng hàng. |
|
KL |
a) b) EG = EH. |
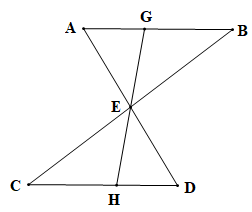
a) Từ AB // CD (theo giả thiết) suy ra (hai góc so le trong) và (hai góc so le trong).
Hay và
Xét tam giác ABE và tam giác DCE có:
(chứng minh trên);
AB = DC (theo giả thiết);
(chứng minh trên).
Vậy (g.c.g).
b) Từ (chứng minh câu a) suy ra AE = DE (hai cạnh tương ứng).
Xét tam giác AEG và tam giác DEH có:
(do );
AE = DE (chứng minh trên);
(hai góc đối đỉnh).
Vậy (g.c.g).
Suy ra EG = EH (hai cạnh tương ứng).
Xem thêm lời giải bài tập SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác




