Hàm số nào sau đây có cực đại, cực tiểu và
B. \(y = - {x^3} + 9{x^2} + 3x + 2\)
D. \(y = {x^3} - 9{x^2} - 3x + 5\)
Đáp án B
Phương pháp:
Đồ thị hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d,\,\,\,\left( {a \ne 0} \right)\) có 2 điểm cực trị:
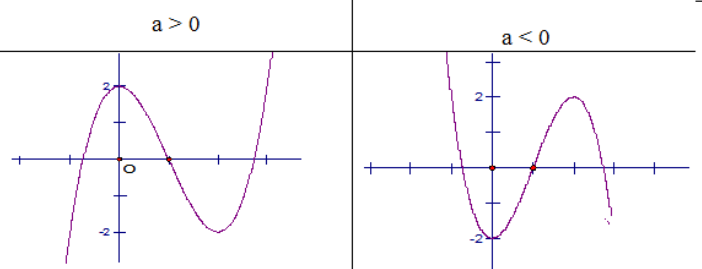
Khi đó để hàm số có thì \(a < 0\)
Cách giải:
Hàm số có thì \(a < 0 \Rightarrow \)Loại bỏ phương án C và D.
+) Xét \(y = - {x^3} - 3x - 2 \Rightarrow y' = - 3{x^2} - 3,\,\,y' = 0\): vô ngiệm \( \Rightarrow \) Hàm số không có cực trị \( \Rightarrow \)Loại bỏ phương án A.
+) \(y = - {x^3} + 9{x^2} + 3x + 2 \Rightarrow y' = - 3{x^2} + 18x + 3,\,\,\,y' = 0\) có hai nghiệm phân biệt thỏa mãn yêu cầu đề bài.