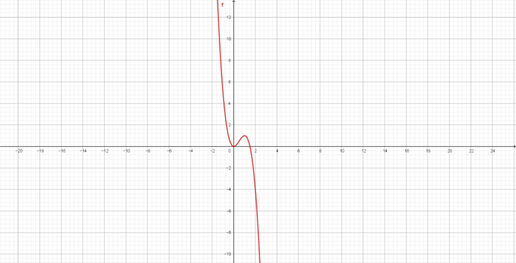
Hàm đồ thị (C):y = x^3 - 3x^2. Có bao nhiêu số nguyên b thuộc ( - 10;10) để có đúng một tiếp tuyến của (C) qua (0;b) A. 9 B. 16 C. 2 D. 17
43
27/04/2024
Hàm đồ thị \((C):y = {x^3} - 3{x^2}.\) Có bao nhiêu số nguyên \(b \in ( - 10;10)\) để có đúng một tiếp tuyến của \((C)\) qua \((0;b)\)
A. \(9\).
B. \(16\) .
C. \(2\) .
D. \(17\).
Trả lời
Lời giải
Chọn D
Ta có \(y' = 3{x^2} - 6x\).
Phương trình tiếp tuyến với \((C)\) tại điểm \(M({x_0};{x_0}^3 - 3{x_0})\) là
\(y = \left( {3{x_0}^2 - 6{x_0}} \right)(x - {x_0}) + {x_0}^3 - 3{x_0}^2.\)
Tiếp tuyến qua \((0;b) \Leftrightarrow \left( {3{x_0}^2 - 6{x_0}} \right)(0 - {x_0}) + {x_0}^3 - 3{x_0}^2 = b \Leftrightarrow b = - 2{x_0}^3 + 3{x_0}^2\).
Có đúng một tiếp tuyến của \((C)\)qua \((0;b)\)\( \Leftrightarrow b = - 2{x_0}^3 + 3{x_0}\) có đúng một nghiệm \({x_0}.\)
Dựa vào đồ thị của hàm số \(f(t) = - 2{t^3} + 3{t^2}\) suy ra có 17 số nguyên \(b \in {\rm{[}} - 9;9]\backslash {\rm{\{ }}0;1\} \) để đồ thị hàm số \(y = - 2{x^3} + 3{x^2}\) cắt đường thẳng \(y = b\) tại đúng một điểm.
Chọn đáp án D.